
| A. | 4 | B. | $\frac{9}{2}$ | C. | $\frac{7}{2}$ | D. | 3 |
分析 根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标的和,求出线段AB的中点到y轴的距离.
解答 解:∵F是抛物线y2=2x的焦点,
∴F($\frac{1}{2}$,0),准线方程x=-$\frac{1}{2}$,
设A(x1,y1),B(x2,y2),
∴|AF|+|BF|=x1+$\frac{1}{2}$+x2+$\frac{1}{2}$=8,
∴x1+x2=7,
∴线段AB的中点横坐标为$\frac{7}{2}$,
∴线段AB的中点到y轴的距离为$\frac{7}{2}$.
故选:C
点评 本题考查解决抛物线上的点到焦点的距离问题,解题的关键是利用抛物线的定义将到焦点的距离转化为到准线的距离.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
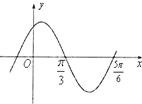 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到函数y=cos(2x+$\frac{π}{6}$)的图象,只需将y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到函数y=cos(2x+$\frac{π}{6}$)的图象,只需将y=f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,正视图与俯视图完全相同,则该几何体的体积为( )
某几何体的三视图如图所示,正视图与俯视图完全相同,则该几何体的体积为( )| A. | $\frac{56π}{3}$ | B. | $\frac{192-8π}{3}$ | C. | $\frac{64-8π}{3}$ | D. | 16+16$\sqrt{5}$+4($\sqrt{2}$-1)π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com