
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| x |
| a |
| y |
| b |
| EM |
| EM |
| c |
| a |
| ||
| 3 |
| |bc| | ||
|
|
| EM |
| EN |
| 5 |
| 9 |
| 7 |
| 3 |
| c |
| a |
| ||
| 3 |
| ||
| 3 |
| x |
| a |
| y |
| b |
| |bc| | ||
|

| x2 |
| 6 |
| y2 |
| 2 |
|
| 12k2 |
| 1+3k2 |
| 12k2-6 |
| 1+3k2 |
| EM |
| EN |
| EM |
| EN |
| 12k2-6 |
| 1+3k2 |
| 12k2 |
| 1+3k2 |
| (3m2-12m+10)k2+(m2-6) |
| 3k2+1 |
| 7 |
| 3 |
| EM |
| EN |
| 5 |
| 9 |
| 7 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 居民区 | 低保户数 | 抽取低保户数 |
| A | 34 | 2 |
| B | 17 | x |
| C | 68 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:
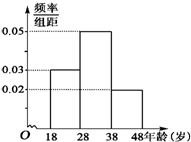 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:| 组数 | 分组 | 回答正确的人数 | 占本组的频率 |
| 第1组 | [18,28) | 240 | x |
| 第2组 | [28,38) | 300 | 0.6 |
| 第3组 | [38,48] | a | 0.4 |
| t-40 |
查看答案和解析>>
科目:高中数学 来源: 题型:
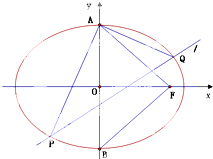 如图所示,A、B分别是椭圆C:
如图所示,A、B分别是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com