练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析，随机抽取了15分到45分之间的1000名学员的成绩，并根据这1000名驾驶员的成绩画出样本的频率分布直方图（如图），则成绩在[30，35）内的驾驶员人数共有300．

    分析 结合图形，求出成绩在[30，35）内的驾驶员人数的频率，即可求出成绩在[30，35）内的驾驶员人数．

    解答 解：根据题意，成绩在[30，35）内的驾驶员人数的频率为
    1-（0.01+0.01+0.04+0.05+0.03）×5=1-0.7=0.3，
    ∴成绩在[30，35）内的驾驶员人数为：1000×0.3=300；
    故答案为：300．

    点评 本题考查了频率分布直方图的应用问题，解题过程中应会识图、用图，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知数列{an}的前n项和Sn=$\frac{n（n+1）}{2}$．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=（-1）n（an•${2^{a_n}}$+$\frac{1}{{\sqrt{{a_{n+1}}}-\sqrt{a_n}}}$），求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知集合A={x|x2-1≥0，x∈R}，B={x|0≤x＜3，x∈R}，则A∩B=（　　）
    A．{x|1＜x＜3，x∈R}B．{x|1≤x≤3，x∈R}C．{x|1≤x＜3，x∈R}D．{x|0＜x＜3，x∈R}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知集合M={x|lnx＞0}，N={x|x2≤4}，则M∩N=（　　）
    A．（1，2]B．[1，2）C．（1，2）D．[1，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设i是虚数单位，$\overline{z}$表示复数z的共轭复数，且满足z+$\overline{z}$=z•$\overline{z}$=2，则z的虚部是（　　）
    A．1B．±iC．±1D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上存在四个不同的点A、B、C、D，使四边形ABCD为菱形，则$\frac{b}{a}$的取值范围为$\frac{b}{a}$＞1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

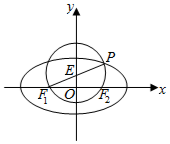    1．如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与圆E：x2+y2-y-2=0在第一象限相交于点P，椭圆C的左、右焦点F1，F2都在圆E上，且线段PF1为圆E的直径．
    （1）求椭圆C的方程；
    （2）设直线l与椭圆C相交于A，B两点，且直线l与y轴相交于D点，M为线段AB的中点，O为坐标原点，若$\overrightarrow{OM}$•$\overrightarrow{OD}$=1，求|OM|•|AB|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．若数列{an}满足：an+1+（-1）nan=n（n∈N*），则a1+a2+…+a100=2550．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，过点F向C的一条渐近线引垂线，垂足为M，交另一条渐近线于点N，若3$\overrightarrow{MF}$=$\overrightarrow{FN}$，则双曲线C的离心率是$\frac{\sqrt{6}}{2}$．

    查看答案和解析>>

    同步练习册答案