
【题目】如图,在四棱锥![]() 中,
中, ![]()
![]() ,底面
,底面![]() 是矩形,
是矩形, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
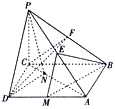
(1)求证:![]() ;
;
(2)已知点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一动点,当
上一动点,当![]() 为何值时,平面
为何值时,平面![]() ?
?
【答案】(1)证明见解析;(2)当![]() 时,平面
时,平面![]() .
.
【解析】试题分析:(1)根据线面垂直的判定定理,若证![]() 平面
平面![]() ,则须证
,则须证![]() 垂直于平面
垂直于平面![]() 内的两条相交直线.根据题意,易证
内的两条相交直线.根据题意,易证![]() ,
, ![]() ,又
,又![]() ,从而问题可得证;(2)根据题意,过点
,从而问题可得证;(2)根据题意,过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,因为
,因为![]() 是
是![]() 的中点,所以易证平面
的中点,所以易证平面![]() 平面
平面![]() ,即平面
,即平面![]() 平面
平面![]() ,又在矩形
,又在矩形![]() 中,易求得
中,易求得![]() ,当
,当![]() 是
是![]() 与
与![]() 的交点时,即
的交点时,即![]() 时,平面
时,平面![]() .
.
试题解析:(1)证明:∵![]() ,底面
,底面![]() 是矩形,
是矩形,
∴![]() ,又
,又![]() ,∴
,∴![]() ,………………2分
,………………2分
∴![]() .………………………………………………4分
.………………………………………………4分
∵![]() ,
, ![]() 为
为![]() 的中点,∴
的中点,∴![]() .………………………………5分
.………………………………5分
∵![]() ,∴
,∴![]() .……………………………………6分
.……………………………………6分
(2)过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,………………………………7分
,………………………………7分

∵∴![]() ,……………………………………8分
,……………………………………8分
∵![]() ,∴
,∴![]() ,……………………………………9分
,……………………………………9分
∴当![]() 是
是![]() 与
与![]() 的交点时,平面
的交点时,平面![]() ,…………………………………………10分
,…………………………………………10分
在矩形![]() 中,求得
中,求得![]() .……………………………………12分
.……………………………………12分


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知长方形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
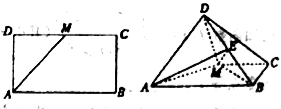
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,三棱锥
在何位置时,三棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积之比为1:3?
的体积之比为1:3?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且首项a1≠3,an+1=Sn+3n(n∈N*).
(1)求证:数列{Sn-3n}是等比数列;
(2)若{an}为递增数列,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查表明,高三学生的幸福感与成绩,作业量,人际关系的满意度的指标有极强的相关性,现将这三项的满意度指标分别记为![]() ,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标
,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意.再用综合指标![]() 的值评定高三学生的幸福感等级:若
的值评定高三学生的幸福感等级:若![]() ,则幸福感为一级;若
,则幸福感为一级;若![]() ,则幸福感为二级;若
,则幸福感为二级;若![]() ,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
,则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况,研究人员随机采访了该群体的10名高三学生,得到如下结果:
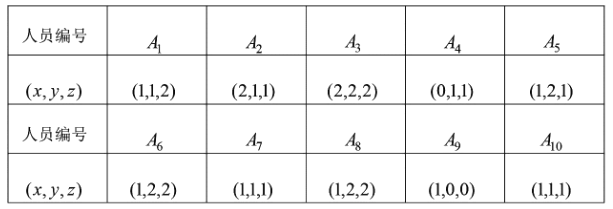
(1)在这10名被采访者中任取两人,求这两人的成绩满意度指标![]() 相同的概率;
相同的概率;
(2)从幸福感等级是一级的被采访者中任取一人,其综合指标为![]() ,从幸福感等级不是一级的被采访者中任取一人,其综合指标为
,从幸福感等级不是一级的被采访者中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求
,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个质地均匀的正四面体骰子,每个面上分别标有数字1、2、3、4,将这个骰子连续投掷两次,朝下一面的数字分别记为![]() ,试计算下列事件的概率:
,试计算下列事件的概率:
(1)事件![]() ;
;
(2)事件![]() :函数
:函数![]() 在区间
在区间![]() 上为增函数.
上为增函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com