
分析 (Ⅰ)由曲线C1普通方程为x+y=6可得曲线C1的极坐标方程;先将曲线C2化为x2+y2-2y=0,进而可得曲线C2的极坐标方程;
(Ⅱ)设A(ρ1,α),B(ρ2,α),0<α<$\frac{3π}{4}$,则ρ1=$\frac{6}{cosα+sinα}$,ρ2=2sinα,可得$\frac{|OB|}{|OA|}$=$\frac{1}{3}$sinα(cosα+sinα),进而得到答案.
解答 解:(Ⅰ)曲线C1:$\left\{\begin{array}{l}{x=3-t}\\{y=3+t}\end{array}\right.(t为参数)$,普通方程为x+y=6,极坐标方程为ρcosθ+ρsinθ=6;
曲线C2:x2+(y-1)2=1,即x2+y2-2y=0,∴ρ=2sinθ;
(Ⅱ)设A(ρ1,α),B(ρ2,α),0<α<$\frac{3π}{4}$,
则ρ1=$\frac{6}{cosα+sinα}$,ρ2=2sinα,…(6分)
$\frac{|OB|}{|OA|}$=$\frac{1}{3}$sinα(cosα+sinα)
=$\frac{1}{6}$(sin2α+1-cos2α)=$\frac{1}{6}$[$\sqrt{2}$sin(2α-$\frac{π}{4}$)+1],…(8分)
当α=$\frac{3π}{8}$时,$\frac{|OB|}{|OA|}$取得最大值$\frac{1}{6}$($\sqrt{2}$+1).…(10分)
点评 本题考查的知识点是直线与圆的极坐标方程,圆的参数方程,三角函数的最值,难度中档.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
已知五边形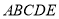 由直角梯形
由直角梯形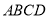 与直角△
与直角△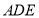 构成,如图1所示,
构成,如图1所示,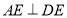 ,
,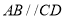 ,
,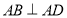 ,且
,且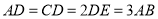 ,将梯形
,将梯形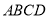 沿着
沿着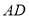 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面
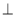 平面
平面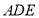 .
.
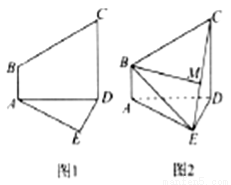
(1)在线段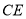 上存在点
上存在点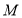 ,且
,且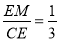 ,证明:
,证明: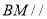 平面
平面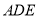 ;
;
(2)求二面角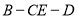 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{7\sqrt{2}}{2}$ | D. | $\frac{7\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com