
分析 由于tanx=2,将所求关系式的分母除以1=sin2x+cos2x,“弦”化“切”后,将tanx=2代入计算即可.
解答 解:∵tanx=2,
∴2sin2x-3sinxcosx+cos2x
=$\frac{2si{n}^{2}x-3sinxcosx+co{s}^{2}x}{si{n}^{2}x+co{s}^{2}x}$
=$\frac{2ta{n}^{2}x-3tanx+1}{ta{n}^{2}x+1}$
=$\frac{8-6+1}{4+1}$
=$\frac{3}{5}$.
点评 本题考查三角函数的化简求值,将所求关系式的分母除以1=sin2x+cos2x,“弦”化“切”是关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8$\sqrt{2}$ | B. | 16$\sqrt{2}$ | C. | 32$\sqrt{2}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
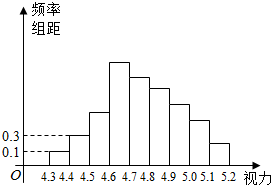 为了解某校学生的视力情况,随机抽查了该校的100名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87,设最大频率a视力在4.5到5.2之间的学生数b,则a,b的值分别为( )
为了解某校学生的视力情况,随机抽查了该校的100名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87,设最大频率a视力在4.5到5.2之间的学生数b,则a,b的值分别为( )| A. | 0.27,96 | B. | 0.27,83 | C. | 2.7,78 | D. | 2.7,83 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com