
| A. | 命题“p∨q”为假 | B. | 命题“p∧q”为真 | C. | 命题“p∨¬q”为假 | D. | 命题“p∧¬q”为真 |
分析 命题p:由已知可得α∥β或相交,即可得出真假;命题q:向量$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(λ,1)的夹角为钝角的充要条件为$\left\{\begin{array}{l}{\overrightarrow{a}•\overrightarrow{b}<0}\\{且不异向共线}\end{array}\right.$,解出即可判断出真假.再利用复合命题真假的判定方法即可得出.
解答 解:命题p:若平面α与平面β不重合,且平面α内有不共线的三点到平面β的距离相等,则α∥β或相交,因此是假命题;
命题q:向量$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(λ,1)的夹角为钝角的充要条件为$\left\{\begin{array}{l}{\overrightarrow{a}•\overrightarrow{b}<0}\\{且不异向共线}\end{array}\right.$,-2λ-1<0,解得$λ>-\frac{1}{2}$,由-λ+2=0,解得λ=2,此时$\overrightarrow{a}$与$\overrightarrow{b}$异向共线,因此向量$\overrightarrow{a}$=(-2,-1),$\overrightarrow{b}$=(λ,1)的夹角为钝角的充要条件为λ∈(-$\frac{1}{2}$,+∞)且λ≠2,因此是假命题.
关于以上两个命题,下列结论中正确的是“p∨q”为假命题.
故选:A.
点评 本题考查了不等式的解法、简易逻辑的判定方法、向量数量积运算性质、空间位置关系的判定,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
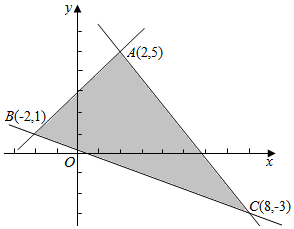 直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示:
直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
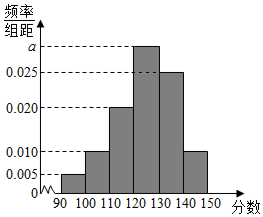 某高校从2015年招收的大一新生中,随机抽取60名学生,将他们的2015年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2015年招收的大一新生中,随机抽取60名学生,将他们的2015年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com