
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),直线
(t为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)写出![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() ,
,![]() 为
为![]() 与
与![]() 的交点,求
的交点,求![]() 的极径.
的极径.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x-2)①与x=-2+ky②;联立①②,消去k可得C的普通方程为x2-y2=4;
(2)将l的极坐标方程与曲线C的极坐标方程联立,可得关于θ的方程,解得tanθ,即可求得l与C的交点M的极径为ρ.
(1)消去参数t,得l1的普通方程l1:y=k(x-2);
消去参数m,得l2的普通方程l2:y=![]() (x+2). 设P(x,y),由题设得
(x+2). 设P(x,y),由题设得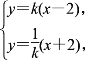
消去k,得x2-y2=4(y≠0),所以C的普通方程为x2-y2=4(y≠0).
(2)C的极坐标方程为ρ2(cos2θ-sin2θ)=4(0<θ<2π,θ≠π),
联立![]() 得cos θ-sin θ=2(cos θ+sin θ).
得cos θ-sin θ=2(cos θ+sin θ).
故tan θ=-![]() ,从而cos2θ=
,从而cos2θ=![]() ,sin2θ=
,sin2θ=![]() .
.
代入ρ2(cos2θ-sin2θ)=4,得ρ2=5,所以l与C的交点M的极径为![]() .
.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】近年来,石家庄经济快速发展,跻身新三线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,石家庄的交通优势在同级别的城市内无能出其右.为了调查石家庄市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
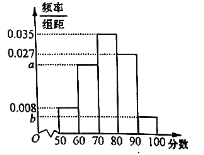
(1)求![]() ,
,![]() 的值;
的值;
(2)求被调查的市民的满意程度的平均数,中位数(保留小数点后两位),众数;
(3)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:
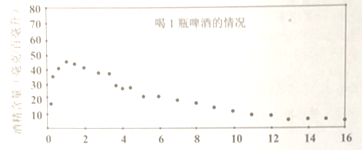
该函数模型如下:
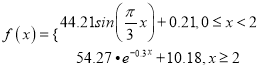
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜奶店每天购进30瓶鲜牛奶,且当天的利润y(单位:元)关于当天需求量n(单位:瓶,n∈N)的函数解析式![]() (n∈N).鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶)绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5):
(n∈N).鲜奶店记录了100天鲜牛奶的日需求量(单位:瓶)绘制出如下的柱形图(例如:日需求量为25瓶时,频数为5):
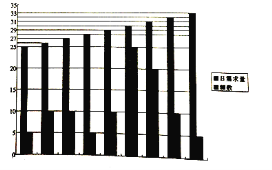
(1)求这100天的日利润(单位:元)的平均数;
(2)以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 |
产品销量y(件) | q | 85 | 82 | 80 | 75 |
已知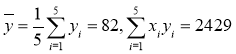
(1)求出q的值;
(2)已知变量![]() 具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程
具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(3)假设试销单价为10元,试估计该产品的销量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com