练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

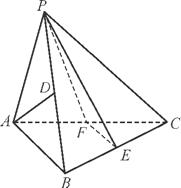
     如图,在三棱锥P-ABC中,BC⊥平面PAB.已知PA=AB,点D,E分别为PB,BC的中点.

    (1) 求证:AD⊥平面PBC;

    (2) 若点F在线段AC上,满足AD∥平面PEF,求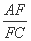的值.


     (1) 证明略　(2) =


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知矩阵M=对应的变换将点A(1,1)变为A'(0,2),将曲线C:xy=1变为曲线C',求:

    (1) 实数a,b的值;

    (2) 曲线C'的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)=sin2ωx+2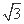sinωx·cosωx-cos2ωx+λ (x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈.

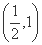    (1) 求函数f(x)的最小正周期;

    (2) 若y=f(x)的图象经过点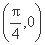,求函数f(x)的值域.

    三角函数的求值与化简

    查看答案和解析>>

    科目：高中数学 来源： 题型：


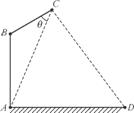
    在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与道路垂直,且∠ABC=120°,路灯C采用锥形灯罩,射出的光线如图中阴影部分所示,已知∠ACD=60°,路宽AD=24 m,设灯柱高AB=h(m),∠ACB=θ(30°≤θ≤45°).

    (1) 求灯柱的高h(用θ表示);

    (2) 若灯杆BC与灯柱AB所用材料相同,记此用料长度和为S,求S关于θ的函数解析式,并求出S的最小值.

    　(第11题)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


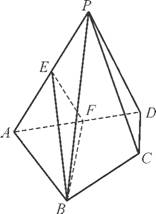
    如图,在四棱锥PABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:

    (1) 直线EF∥平面PCD;

    (2) 平面BEF⊥平面PAD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有如下命题:

    ①过平面外一点有且只有一条直线与该平面垂直;

    ②过平面外一点有且只有一条直线与该平面平行;

    ③如果两个平行平面和第三个平面相交, 那么所得的两条交线平行;

    ④如果两个平面相互垂直, 那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内.则所有真命题的序号是　　　　.(填序号) 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设Sn是公差不为0的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正项数列{an}满足Sn=.

    (1) 求a1,a2,a3并推测an;

    (2) 用数学归纳法证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若随机变量X的概率分布为P(X=k)=,k=1,2,3,4,其中c是常数,则P<X<的值为　　　　.

    查看答案和解析>>

    同步练习册答案