考点:数列递推式,数列与不等式的综合
专题:点列、递归数列与数学归纳法,不等式的解法及应用
分析:(Ⅰ)由a
1=3,a
n=
,得
a2=,
a3=,且可知a
n>0.再由a
n=
,两边平方得
an2=an-1+2,进一步得到
an+12=an+2,
两式作差可得a
n+1-a
n与a
n-a
n-1同号.由
a2-a1=-3<0易知,a
n-a
n-1<0,即a
n<a
n-1,可知数列{a
n}单调递减;
(Ⅱ)由
an2=an-1+2,可得,
an2-4=an-1-2,(a
n-2)(a
n+2)=a
n-1-2,进一步得到
|an-2|=.由a
n-2与a
n-1-2同号,可得a
n-2>0,即a
n>2,可得
<,则|a
n-2|<
|a
n-1-2|;
(Ⅲ)由(a
n-2)(a
n+2)=a
n-1-2,得
an+2=,即
bn=,累积后由|a
n-2|<
|a
n-1-2|,可知|a
n-2|<
|a
n-1-2|
<|an-2-2|<|an-3-2|<…<|a1-2|=
,得
>4n-1,由a
n>2,得
>4n-1.结合当n→∞时,4
n-1→∞,说明不存在常数M,对任意n≥2,有b
2b
3…b
n≤M成立.
解答:
(Ⅰ)解:由a
1=3,a
n=
,得
a2=,
a3=,且可知a
n>0.
由a
n=
,得
an2=an-1+2(1),
则有
an+12=an+2(2),
由(2)-(1)得:
an+12-an2=an-an-1,
(a
n+1+a
n)(a
n+1-a
n)=a
n-a
n-1,
∵a
n>0,∴a
n+1-a
n与a
n-a
n-1同号.由
a2-a1=-3<0,
易知,a
n-a
n-1<0,即a
n<a
n-1,可知数列{a
n}单调递减;
(Ⅱ)证明:由
an2=an-1+2,可得,
an2-4=an-1-2,(a
n-2)(a
n+2)=a
n-1-2,
∴
|an-2|=.
由(a
n-2)(a
n+2)=a
n-1-2,易知,a
n-2与a
n-1-2同号,
由于a
1-2=3-2>0,可知,a
n-2>0,即a
n>2,
∴a
n+2>4,∴
<,
∴|a
n-2|<
|a
n-1-2|,得证;
(Ⅲ)解:∵(a
n-2)(a
n+2)=a
n-1-2,
∴
an+2=,即
bn=,
则
b2b3…bn=•…==
.
由|a
n-2|<
|a
n-1-2|,可知,
|a
n-2|<
|a
n-1-2|
<|an-2-2|<|an-3-2|<…<|a1-2|=
,
∴
>4n-1,
∵a
n>2,
∴
>4n-1.
当n→∞时,4
n-1→∞,
故不存在常数M,对任意n≥2,有b
2b
3…b
n≤M成立.
点评:本题是数列与不等式的综合题,考查了数列递推式,训练了累积法求数列的通项公式,训练了放缩法证明数列不等式,属难题.



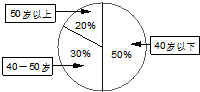 某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )
某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )