
分析 (1)f′(x)=λex-2x,据题意得f′(x)=λex-2x=0有两个不同的根x1,x2,对λ分类讨论:当λ≤0时,可得f(x)在R上递减,不合题意.λ>0,令f″(x)=0,解得$x=ln\frac{2}{λ}$,可得函数f′(x)=λex-2x在$(-∞,ln\frac{2}{λ})$上递减,在$(ln\frac{2}{λ},+∞)$上递增,f′(x)=λex-2x=0有两个不同的根,则${f^/}(ln\frac{2}{λ})<0$,解出即可得出.
(2)当λ=1时,由题意可得:不等式${e^x}>\frac{μ}{2}x-\frac{15}{2}$对任意x恒成立,令$h(x)={e^x}-\frac{μ}{2}x+\frac{15}{2}$,令h′(x)=0得$x=ln\frac{μ}{2}$,利用单调性可得$h{(x)_{min}}=h(ln\frac{μ}{2})=\frac{μ}{2}-\frac{μ}{2}ln\frac{μ}{2}+\frac{15}{2}>0$,整理得φ(u)=$μ-μln\frac{μ}{2}+15>0$,再研究其单调性即可得出.
解答 解:(1)f′(x)=λex-2x,
据题意得f′(x)=λex-2x=0有两个不同的根x1,x2,
当λ≤0时,f′(x)=λex-2x≤0,因此f(x)在R上递减,不合题意,
∴λ>0,
又f″(x)=λex-2,令f″(x)=0,解得$x=ln\frac{2}{λ}$,
∴函数f′(x)=λex-2x在$(-∞,ln\frac{2}{λ})$上递减,在$(ln\frac{2}{λ},+∞)$上递增,
∴f′(x)=λex-2x=0有两个不同的根,则${f^/}(ln\frac{2}{λ})<0$,
即$λ•\frac{2}{λ}-2ln\frac{2}{λ}<0$,$ln\frac{2}{λ}>1$,
解得$0<λ<\frac{2}{e}$.
(2)当λ=1时,求使不等式f(x)>g(x)在一切实数上恒成立,即不等式${e^x}>\frac{μ}{2}x-\frac{15}{2}$对任意x恒成立,
令$h(x)={e^x}-\frac{μ}{2}x+\frac{15}{2}$,∴${h^/}(x)={e^x}-\frac{μ}{2}$,令h′(x)=0得$x=ln\frac{μ}{2}$,
∴函数h(x)在$(-∞,ln\frac{μ}{2})$上递减,在$(ln\frac{μ}{2},+∞)$上递增,
∴$h{(x)_{min}}=h(ln\frac{μ}{2})=\frac{μ}{2}-\frac{μ}{2}ln\frac{μ}{2}+\frac{15}{2}>0$,
整理得$μ-μln\frac{μ}{2}+15>0$.
令$ϕ(μ)=μ-μln\frac{μ}{2}+15$,易得ϕ(μ)在(2,+∞)上递减,
若μ=2e2∈(14,15),ϕ(2e2)=15-2e2>0,
若μ=15,$ϕ(15)=2-ln\frac{15}{2}<0$,
所以满足条件的最大整数μ=14.
点评 本题考查了利用导数研究函数的单调性极值与最值、不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于难题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
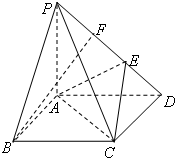 四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=$\sqrt{2}$,E,F为PD上两点,且PF=ED=$\frac{1}{3}$PD.
四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=$\sqrt{2}$,E,F为PD上两点,且PF=ED=$\frac{1}{3}$PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=|x|有极大值,但无极小值 | B. | 函数y=|x|有极小值,但无极大值 | ||
| C. | 函数y=|x|既有极大值又有极小值 | D. | 函数y=|x|无极值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com