
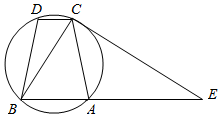
 如图,已知圆内接四边形ABCD满足AC=BD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆内接四边形ABCD满足AC=BD,过C点的圆的切线与BA的延长线交于E点.分析 (1)运用等弧所对的圆周角相等和圆的弦切角定理,即可得证;
(2)由圆的弦切角定理和三角形的相似的判定定理可得△BEC∽△CBD,由性质定理计算即可得到所求BC的长.
解答  解:(1)证明:由AC=BD
解:(1)证明:由AC=BD
即有弧AC的长等于弧BD的长,
可得∠ABC=∠BCD,
又EC为圆的切线,
可得∠ACE=∠ABC,
即有∠ACE=∠BCD,
(2)解:由EC为圆的切线,
可得∠CDB=∠BCE,
由(1)可得∠ABC=∠BCD,
即有△BEC∽△CBD,
可得$\frac{CD}{BC}$=$\frac{BC}{BE}$,
由BE=9,CD=1,
则BC2=CD•BE=9,
即BC=3.
点评 本题考查圆的弦切角定理和三角形相似的判定定理和性质定理的运用,考查推理和运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,-$\frac{7}{2}$] | D. | (-∞,-$\frac{7}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com