
分析 由于512016+a=(52-1)2016+a,按二项式定理展开,根据题意可得${C}_{2016}^{2016}$•(-1)2016+a 能被13整除,再由0≤a<13,确定出a的值.
解答 解:512016+a=(52-1)2016+a
=${C}_{2016}^{0}$•522016+${C}_{2016}^{1}$•522015•(-1)1+${C}_{2016}^{2}$•522014•(-1)2+…+${C}_{2016}^{2016}$•(-1)2016+a,
除最后两项外,其余各项都有13的倍数52,
故由题意可得${C}_{2016}^{2016}$•(-1)2016+a能被13整除,
∵0≤a<13,
∴a=12,
故答案为:12
点评 此题考查了二项式定理的应用,二项式展开式的通项公式,熟练掌握二项式定理是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a,+∞) | |
| B. | (-∞,a) | |
| C. | 当a>1时,解集是(a,+∞);当0<a<1时,解集是(-∞,a) | |
| D. | 当a>1时,解集是(-∞,a);当0<a<1时,解集是(a,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
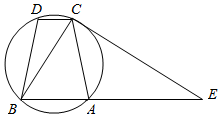 如图,已知圆内接四边形ABCD满足AC=BD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆内接四边形ABCD满足AC=BD,过C点的圆的切线与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com