
分析 (Ⅰ)分类讨论,利用函数f(x)=|x-a|+|${\frac{1}{2}$x+1|的最小值为2,建立方程求实数a的值;
(Ⅱ)由题意,a=2,不等式f(x)≤4,即|x-2|+|${\frac{1}{2}$x+1|≤4,结合图象求不等式f(x)≤4的解集.
解答 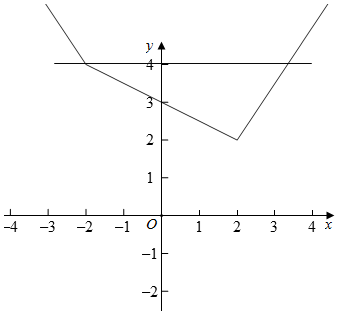 解:(Ⅰ)a≥-2,f(x)=$\left\{\begin{array}{l}{\frac{3}{2}x+1-a,x≥a}\\{-\frac{1}{2}x+1+a,-2≤x≤a}\\{-\frac{3}{2}x+a-1,x≤-2}\end{array}\right.$,
解:(Ⅰ)a≥-2,f(x)=$\left\{\begin{array}{l}{\frac{3}{2}x+1-a,x≥a}\\{-\frac{1}{2}x+1+a,-2≤x≤a}\\{-\frac{3}{2}x+a-1,x≤-2}\end{array}\right.$,
∴f(x)min=1+$\frac{a}{2}$=2,∴a=2;
a≤-2,f(x)=$\left\{\begin{array}{l}{\frac{3}{2}x+1-a,x≥-2}\\{\frac{3}{2}x-a-1,a≤x≤-2}\\{-\frac{3}{2}x+a-1,x≤a}\end{array}\right.$,
∴f(x)min=-1-$\frac{a}{2}$=2,∴a=-6;
(Ⅱ)由题意,a=2,不等式f(x)≤4,即|x-2|+|${\frac{1}{2}$x+1|≤4
x>2时,$\frac{3}{2}$x-1=4,
∴x=$\frac{10}{3}$,-$\frac{1}{2}x+3=4$,
∴x=-2,
∵|x-2|+|${\frac{1}{2}$x+1|≤4,
∴不等式的解集为[-2,$\frac{10}{3}$].
点评 本题考查绝对值函数,考查绝对值不等式的解法,考查数形结合的数学思想,属于中档题.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:选择题
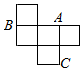 一个无盖的正方体盒子展开后的平面图如图所示,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的度数是( )
一个无盖的正方体盒子展开后的平面图如图所示,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的度数是( )| A. | 45° | B. | 30° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
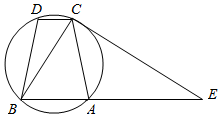 如图,已知圆内接四边形ABCD满足AC=BD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆内接四边形ABCD满足AC=BD,过C点的圆的切线与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
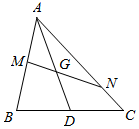 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com