
���� ��1����x=��cos�ȣ�y=��sin�ȣ�x2+y2=��2��������C1�ķ���Ϊ��x-1��2+y2=1������ͼ��仯�ɵĹ��ɿɵ�����C��
��2����ֱ��l�IJ������̴�������C�ķ��̣�$\frac{{x}^{2}}{4}+{y}^{2}=1$�У���$\frac{5}{2}{t}^{2}+2t-2=0$������Τ�ﶨ���������ļ������壬������|PA|+|PB|��
��� �⣺��1������C1��ֱ�����귽��Ϊ��x2+y2-2x=0����x-1��2+y2=1��
������C�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$
������C��ʾ��������Ϊ��$-\sqrt{3}$��0������$\sqrt{3}$��0�������᳤Ϊ4����Բ
��2����ֱ��l�IJ������̴�������C�ķ��̣�$\frac{{x}^{2}}{4}+{y}^{2}=1$�У���$\frac{5}{2}{t}^{2}+2t-2=0$��
��A��B�����Ӧ�IJ����ֱ�Ϊt1��t2
��t1+t2=-$\frac{4}{5}$��t1t2=-$\frac{4}{5}$��
��|PA|+|PB|=|t1|+|t2|=|t1-t2|=$\frac{4\sqrt{6}}{5}$
���� ���⿼�鼫���귽�̺�ֱ�����귽�̵Ļ���������ֱ�ߵIJ������̵����ã��Լ�Τ�ﶨ�������Һ�������ֵ�����ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��+�ޣ� | |
| B�� | ��-�ޣ�a�� | |
| C�� | ��a��1ʱ���⼯�ǣ�a��+�ޣ�����0��a��1ʱ���⼯�ǣ�-�ޣ�a�� | |
| D�� | ��a��1ʱ���⼯�ǣ�-�ޣ�a������0��a��1ʱ���⼯�ǣ�a��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $-\sqrt{3}$ | C�� | $\frac{{\sqrt{3}}}{3}$ | D�� | $-\frac{{\sqrt{3}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
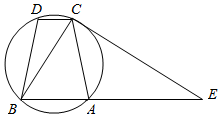 ��ͼ����֪Բ�ڽ��ı���ABCD����AC=BD����C���Բ��������BA���ӳ��߽���E�㣮
��ͼ����֪Բ�ڽ��ı���ABCD����AC=BD����C���Բ��������BA���ӳ��߽���E�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
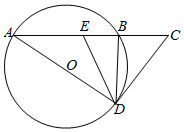 ��ͼ��A��B��ԲO�����㣬�ӳ�AB����C������AB=2BC=2����C��ֱ��CD��ԲO�����ڵ�D����ADB��ƽ���߽�AB�ڵ�E��
��ͼ��A��B��ԲO�����㣬�ӳ�AB����C������AB=2BC=2����C��ֱ��CD��ԲO�����ڵ�D����ADB��ƽ���߽�AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com