
| x | -$\frac{��}{6}$ | $\frac{��}{3}$ | $\frac{5��}{6}$ | $\frac{4��}{3}$ | $\frac{11��}{6}$ | $\frac{7��}{3}$ | $\frac{17��}{6}$ |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
���� ��1�����ݱ����ṩ�����ݣ����T���غ�A��B��ֵ��д��f��x���Ľ���ʽ���ɣ�
��2���������Һ�����ͼ�������ʣ��������f��x�� �ĵ����������䣻
��3���ɺ���y=f��kx������С���������k��ֵ�������û�Ԫ������t=3x-$\frac{��}{3}$����Ϻ�����ͼ���������f��kx��=mǡ��������ͬ�Ľ�ʱm��ȡֵ��Χ��
��� �⣺��1�����ݱ����ṩ�����ݣ���T=2��[$\frac{5��}{6}$-��-$\frac{��}{6}$��]=2�У�
�֦أ�0��
���=$\frac{2��}{T}$=1��
��A=2��B=1��
��f��x��=2sin��x+�գ�+1��
��f��$\frac{5��}{6}$��=2sin��$\frac{5��}{6}$+�գ�+1=3��
��|��|��$\frac{��}{2}$�����=-$\frac{��}{3}$��
����y=f��x���Ľ���ʽΪf��x��=2sin��x-$\frac{��}{3}$��+1��
��2����-$\frac{��}{2}$+2k��x-$\frac{��}{3}$��$\frac{��}{2}$+2k��k��Z��
���-$\frac{��}{6}$+2k��x��$\frac{5��}{6}$+2k��
�ຯ��f��x�� �ĵ�����������Ϊ��[-$\frac{��}{6}$+2k�У�$\frac{5��}{6}$+2k��]����k��Z����
��3������֪�ú���y=f��kx��=2sin��kx-$\frac{��}{3}$��+1����С������Ϊ$\frac{2��}{3}$��
��$\frac{2��}{|k|}$=$\frac{2��}{3}$��
��k��0����k=3��
��t=3x-$\frac{��}{3}$��x��[0��$\frac{��}{3}$]��
��t��[-$\frac{��}{3}$��$\frac{2��}{3}$]��
�ֺ���y=sint��[-$\frac{��}{3}$��$\frac{��}{2}$]�ϵ�����������[$\frac{��}{2}$��$\frac{2��}{3}$]�ϵ����ݼ���
��sin$\frac{��}{3}$=sin$\frac{2��}{3}$=$\frac{\sqrt{3}}{2}$����ͼ��ʾ��
��sint=s��[-$\frac{��}{3}$��$\frac{2��}{3}$]����������ͬ�Ľ⣬�ȼ��ں���y=sint��y=s��ͼ����������ͬ�Ľ��㣬
��s��[$\frac{\sqrt{3}}{2}$��1����
���f��kx��=mǡ��������ͬ�Ľ⣬ʵ��m��ȡֵ��Χ��[$\sqrt{3}$+1��3����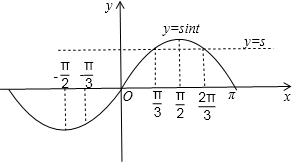
���� ���⿼�������Ǻ�����ͼ�������ʵ�Ӧ�����⣬Ҳ�����˺����뷽�̵�Ӧ�����⣬���ۺ�����Ŀ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 1 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | ��4 | C�� | $2\sqrt{3}$ | D�� | ��$2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com