
分析 利用诱导公式和二倍角公式化简,构造tanα,可得答案.
解答 解:由$cos2α+sin({\frac{π}{2}+α})cos({\frac{3π}{2}-α})$=$\frac{co{s}^{2}α-si{n}^{2}α-cosαsinα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{1-ta{n}^{2}α-tanα}{ta{n}^{2}α+1}$,
∵tanα=2,
∴$cos2α+sin({\frac{π}{2}+α})cos({\frac{3π}{2}-α})$=$\frac{1-4-2}{4+1}=-1$.
故答案为:-1.
点评 本题主要考察了同角三角函数关系式和诱导公式和二倍角公式化简应用,属于基本知识的考查.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
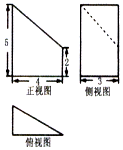
| A. | 45 | B. | $45+\frac{{9\sqrt{2}}}{2}$ | C. | $\frac{117}{2}$ | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{24}{5}$ | C. | $\frac{{2\sqrt{3}}}{5}$ | D. | $\frac{19}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com