
| A. | 45 | B. | $45+\frac{{9\sqrt{2}}}{2}$ | C. | $\frac{117}{2}$ | D. | 60 |
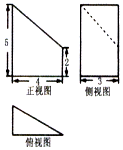
分析 由已知中的三视图,可知该几何体是一个以边长为3,和4的直角三角形为底面的三棱柱,切去了一个边长为3,和4的直角三角形为底面,高是3的三棱锥,累加各个面的面积可得,几何体的表面积.
解答 解:由已知中的三视图,可知该几何体是一个以边长为3,和4的直角三角形为底面的三棱柱,切去了一个边长为3,和4的直角三角形为底面,高是3的三棱锥. (如图)ABC-D是切去的三棱锥
(如图)ABC-D是切去的三棱锥
可得:矩形ABB′A′的面积为:5×3=15,
梯形ADC′A′的面积为:$\frac{1}{2}(5+2)×5$=$\frac{35}{2}$,
梯形BDC′B′的面积为:$\frac{1}{2}(5+2)×4=14$,
底面ABC的面积为:$3×4×\frac{1}{2}=6$,
三角形ABD是直角三角形:其面积为:$\frac{1}{2}×3×5=\frac{15}{2}$,
∴该几何体的表面积为:$\frac{35}{2}+\frac{15}{2}+14+6=45$.
故选A
点评 本题考查的知识点是由三视图求表面积,解决本题的关键是得到该几何体的形状.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 传承传统文化再掀热潮,在刚刚过去的新春假期中,央视科教频道以诗词知识竞赛为 主的《中国诗词大会》火爆荧屏,如图的茎叶图是两位选手在个人追逐赛中的比赛得 分,则下列说法正确的是( )
传承传统文化再掀热潮,在刚刚过去的新春假期中,央视科教频道以诗词知识竞赛为 主的《中国诗词大会》火爆荧屏,如图的茎叶图是两位选手在个人追逐赛中的比赛得 分,则下列说法正确的是( )| A. | 甲的平均数大于乙的平均数 | B. | 甲的中位数大于乙的中位数 | ||
| C. | 甲的方差大于乙的方差 | D. | 甲的平均数等于乙的中位数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}i$ | B. | $-\frac{1}{2}i$ | C. | $-\frac{5}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},+∞})$ | B. | $({-\frac{3}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-∞,-\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com