
| A. | 4 | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
分析 由题意可设直线AB的方程为:x=my+b,与抛物线方程联立可得根与系数的关系、利用斜率公式得出直线AB过定点M(2,0),再利用三角形的面积计算公式即可得出结论.
解答  解:由题意可设直线AB的方程为:x=my+b
解:由题意可设直线AB的方程为:x=my+b
联立$\left\{\begin{array}{l}{x=my+b}\\{{y}^{2}=4x}\end{array}\right.$,化为y2-4my-4b=0,
∴y1+y2=4m,y1y2=-4b.
∵直线OA,OB的斜率分别为k1,k2,k1•k2=-2.
∴$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-2.
∴y1y2=-8,
∴-4b=-8,
∴b=2.
因此直线AB过定点M(2,0).
∴△AOB面积S=$\frac{1}{2}×2×$|y1-y2|=$\sqrt{16{m}^{2}+32}$
因此当m=0时,△AOB的面积取得最小值4$\sqrt{2}$.
故选:C.
点评 本题综合考查了直线与抛物线相交问题转化为方程联立可得根与系数的关系、斜率公式、三角形的面积计算公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
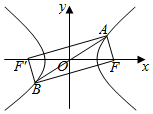 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )| A. | $[{\sqrt{2},\sqrt{3}+1}]$ | B. | $[{\sqrt{3},2+\sqrt{3}}]$ | C. | $[{\sqrt{2},2+\sqrt{3}}]$ | D. | $[{\sqrt{3},\sqrt{3}+1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
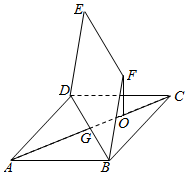 如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | $\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com