
| A. | 2$\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
分析 由题意可知棱锥的四个面全等,棱锥可看做面对角线分别为$\sqrt{3}$,$\sqrt{5}$,$\sqrt{6}$的长方体切去四个全等的小棱锥得到的,使用做差法计算棱锥的体积.
解答 解:∵底面△ABC的每个顶点处的三条棱两两所成的角之和均为180°,
∴三棱锥的三个侧面与底面ABC全等.
∴三棱锥S-ABC可看做是面对角线分别为$\sqrt{3}$,$\sqrt{5}$,$\sqrt{6}$的长方体沿着面对角线切去四个小棱锥得到的几何体.
设长方体的棱长为x,y,z,
则$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=3}\\{{x}^{2}+{z}^{2}=5}\\{{y}^{2}+{z}^{2}=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}^{2}=1}\\{{y}^{2}=2}\\{{z}^{2}=4}\end{array}\right.$,
∴xyz=$\sqrt{{x}^{2}{y}^{2}{z}^{2}}$=2$\sqrt{2}$.
∴三棱锥的体积V=xyz-$\frac{1}{3}×\frac{1}{2}xyz×4$=$\frac{1}{3}xyz$=$\frac{2\sqrt{2}}{3}$.
故选C.
点评 本题考查了棱锥的结构特征和体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
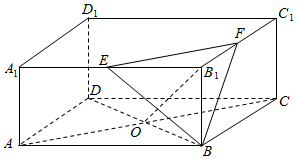 如图,已知长方体ABCD-A1B1C1D1中AB=BC=2,AA1=1,点E,F分别是A1B1,B1C1的中点,点O是AB与BD的交点.
如图,已知长方体ABCD-A1B1C1D1中AB=BC=2,AA1=1,点E,F分别是A1B1,B1C1的中点,点O是AB与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
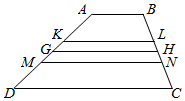 如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.
如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
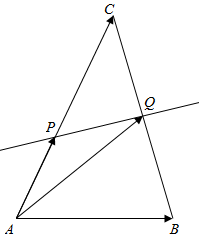 如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.
如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com