
分析 (1)由椭圆经过点(1,$\frac{{\sqrt{6}}}{3}$),离心率为$\frac{{\sqrt{6}}}{3}$,列出方程组求出a,b,由此能求出椭圆C的方程.
(2)由$\overrightarrow{AP}•\overrightarrow{AQ}=0$,知AP⊥AQ,设直线AP的方程为y=kx+1,则直线AQ的方程为$y=-\frac{1}{k}x+1(k≠0)$,将y=kx+1代入椭圆C的方程$\frac{x^2}{3}+{y^2}=1$,得(1+3k2)x2+6kx=0,求出P点坐标,进而求出Q点坐标,由此求出直线l的方程,从而能证明直线l过定点$(0,-\frac{1}{2})$.
解答 解:(1)∵椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)经过点(1,$\frac{{\sqrt{6}}}{3}$),离心率为$\frac{{\sqrt{6}}}{3}$,
∴$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{6}{9{b}^{2}}=1}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得$a=\sqrt{3},b=1$,
∴椭圆C的方程为$\frac{x^2}{3}+{y^2}=1$.…(5分)
证明:(2)由$\overrightarrow{AP}•\overrightarrow{AQ}=0$,知AP⊥AQ,从而直线AP与坐标轴不垂直,
故不妨设直线AP的方程为y=kx+1,则直线AQ的方程为$y=-\frac{1}{k}x+1(k≠0)$,
将y=kx+1代入椭圆C的方程$\frac{x^2}{3}+{y^2}=1$,
并整理得(1+3k2)x2+6kx=0,…(7分)
解得x=0(舍去)或$x=-\frac{6k}{{1+3{k^2}}}$,
因此P的坐标为$(-\frac{6k}{{1+3{k^2}}},-\frac{6k}{{1+3{k^2}}}+1)$,即$(-\frac{6k}{{1+3{k^2}}},\frac{{1-3{k^2}}}{{1+3{k^2}}})$.
将上式中的k换成$-\frac{1}{k}$,得$Q(\frac{6k}{{{k^2}+3}},\frac{{{k^2}-3}}{{{k^2}+3}})$,…(9分)
直线l的方程为$y=\frac{{\frac{{{k^2}-3}}{{{k^2}+3}}-\frac{{1-3{k^2}}}{{1+3{k^2}}}}}{{\frac{6k}{{{k^2}+3}}+\frac{6k}{{1+3{k^2}}}}}(x-\frac{6k}{{{k^2}+3}})+\frac{{{k^2}-3}}{{{k^2}+3}}$,
化简得直线l的方程为$y=\frac{{{k^2}-1}}{4k}x-\frac{1}{2}$,
所以直线l过定点$(0,-\frac{1}{2})$.…(12分)
点评 本题考查椭圆方程的求法,考查直线过定点的证明,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
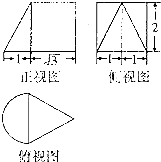
| A. | $\frac{π}{3}$+2$\sqrt{3}$ | B. | $\frac{π}{3}$+$\sqrt{3}$ | C. | π+2$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y-4=0 | B. | 2x+y-4=0 | C. | 2x+3y+4=0 | D. | x+2y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
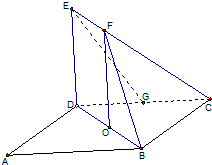 如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.
如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
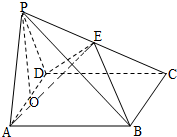 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点,O为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com