
分析 (1)设z=x+yi,x,y∈R,则ω=$x+\frac{9x}{{x}^{2}+{y}^{2}}$+$(y-\frac{9y}{{x}^{2}+{y}^{2}})$i为实数,可得y-$\frac{9y}{{x}^{2}+{y}^{2}}$=0,因此y=0,或x2+y2=9.通过分类讨论即可得出.
(2)由(1)可得:①y=0时,ω=x+$\frac{9}{x}$,由-4<ω<2,可得-4<$x+\frac{9}{x}$<2,利用基本不等式的性质即可得出.②x2+y2=9时.ω=2x,由于-4<ω<2,即可得出x的取值范围.由u=$\frac{α-z}{α+z}$(α>0)为纯虚数,化简可得α,再利用模的计算公式、函数的单调性即可得出.
解答 解:(1)设z=x+yi,x,y∈R,
则ω=z+$\frac{9}{z}$=x+yi+$\frac{9}{x+yi}$=x+yi+$\frac{9(x-yi)}{(x+yi)(x-yi)}$=$x+\frac{9x}{{x}^{2}+{y}^{2}}$+$(y-\frac{9y}{{x}^{2}+{y}^{2}})$i为实数,
∴y-$\frac{9y}{{x}^{2}+{y}^{2}}$=0,∴y=0,或x2+y2=9.
①y=0时,ω=x+$\frac{9}{x}$
∵-2<ω<10,∴-2<$x+\frac{9}{x}$<10,
x>0时,解得1<x<9.x<0时,x∈∅.
综上可得:y=0时,点Z的轨迹方程是$\left\{\begin{array}{l}{y=0}\\{1<x<9}\end{array}\right.$.
②x2+y2=9时.
ω=2x,
∵-2<ω<10,∴-2<2x<10,
解得-1<x<5.
因此x2+y2=9时.可得:点Z的轨迹方程是x2+y2=9(-1<x<5).
(2)由(1)可得:①y=0时,ω=x+$\frac{9}{x}$
∵-4<ω<2,∴-4<$x+\frac{9}{x}$<2,
∵x<0时,$x+\frac{9}{x}$≤-6;x>0时,$x+\frac{9}{x}$≥6.
综上可得:y=0时,x∈∅,点Z的轨迹无方程.
②x2+y2=9时.
ω=2x,
∵-4<ω<2,∴-4<2x<2,
解得-2<x<1.
∵u=$\frac{α-z}{α+z}$(α>0)为纯虚数,
u=$\frac{(α-x-yi)(α+x-yi)}{(α+x+yi)(α+x-yi)}$=$\frac{{α}^{2}-9-2yαi}{{α}^{2}+2αx+9}$,
∴α2-9=0,2yα≠0,
解得α=3,y≠0.
∴u=$\frac{-6yi}{18+6x}$=$\frac{-yi}{3+x}$,
∵x∈(-2,1),
∴|u|=$\sqrt{\frac{{y}^{2}}{(3+x)^{2}}}$=$\sqrt{\frac{3-x}{3+x}}$=$\sqrt{\frac{6}{3+x}-1}$∈$(\frac{\sqrt{2}}{2},\sqrt{5})$.
∴α=3,|u|∈$(\frac{\sqrt{2}}{2},\sqrt{5})$.
点评 本题考查了复数的运算法则、轨迹方程、基本不等式的性质、不等式的解法、函数的单调性,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4029 | B. | 4031 | C. | 4033 | D. | 4035 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2,14,26,38,42,56 | B. | 5,8,31,36,48,54 | ||
| C. | 3,13,23,33,43,53 | D. | 5,10,15,20,25,30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{21}}{2}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
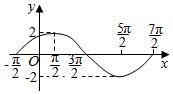 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为f(x)=2sin($\frac{1}{2}$x+$\frac{π}{4}$)..直线y=$\sqrt{3}$与函数y=f(x)(x∈R)图象的所有交点的坐标为($\frac{π}{6}$+4kπ,$\sqrt{3}$)或($\frac{5π}{6}$+4kπ,$\sqrt{3}$)(k∈Z).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为f(x)=2sin($\frac{1}{2}$x+$\frac{π}{4}$)..直线y=$\sqrt{3}$与函数y=f(x)(x∈R)图象的所有交点的坐标为($\frac{π}{6}$+4kπ,$\sqrt{3}$)或($\frac{5π}{6}$+4kπ,$\sqrt{3}$)(k∈Z).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com