
【题目】已知函数![]() ,
, ![]() .
.![]()
(Ⅰ)求![]() 的最大值;
的最大值;
(Ⅱ)若![]() ,判断
,判断![]() 的单调性;
的单调性;
(Ⅲ)若![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)最大值f(e)=![]() ;(Ⅱ)见解析;(III)
;(Ⅱ)见解析;(III)![]() .
.
【解析】试题分析:
(Ⅰ)求解导函数有f′(x)=![]() (x>0),由导函数研究函数的单调性可得当x=e时,f(x)取得最大值f(e)=
(x>0),由导函数研究函数的单调性可得当x=e时,f(x)取得最大值f(e)=![]() .
.
(Ⅱ)a=1, ![]() ,令
,令![]() ,则
,则![]() ,
, ![]() ,则
,则![]() .
. ![]() 在x>0时单调递减.
在x>0时单调递减.
(III)令![]() ,原问题等价于h(x)有两个零点,
,原问题等价于h(x)有两个零点, ![]() ,
,
结合(Ⅰ)的结论可得![]() .
.
试题解析:
(Ⅰ)f′(x)=![]() (x>0),
(x>0),
当x∈(0,e)时,f′(x)>0,f(x)单调递增;
当x∈(e,+∞)时,f′(x)<0,f(x)单调递减,
所以当x=e时,f(x)取得最大值f(e)=![]() .
.
(Ⅱ)a=1, ![]() ,令
,令![]() ,
,
![]() ,当
,当![]() ,
,
当![]() ,
, ![]() ,即
,即![]() ,
,
![]() .故
.故![]() 在x>0时单调递减.
在x>0时单调递减.
(III)![]() g(x)有两个零点等价于h(x)有两个零点,
g(x)有两个零点等价于h(x)有两个零点,
![]() 由(1)知
由(1)知![]() ,
,
由![]() 图像可知
图像可知![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切并且与圆
内切并且与圆![]() 外切,圆心
外切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)已知曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,过动点
两点,过动点![]() 的直线与
的直线与![]() 交于
交于![]() (不垂直
(不垂直![]() 轴),过
轴),过![]() 作直线交
作直线交![]() 于点
于点![]() 且交
且交![]() 轴于点
轴于点![]() ,若
,若![]() 构成以
构成以![]() 为顶点的等腰三角形,证明:直线
为顶点的等腰三角形,证明:直线![]() ,
, ![]() 的斜率之积为定值.
的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
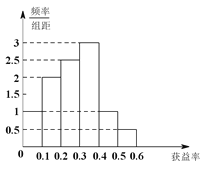
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]() .
.
(i)求参数![]() 的估计值;
的估计值;
(ii)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—5:不等式选讲
已知函数(x)=|2x-a|+ |x -1|.
(Ⅰ)当a=3时,求不等式(x)≥2的解集;
(Ⅱ)若(x)≥5-x对![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面结论正确的是( )
①“所有2的倍数都是4的倍数,某数![]() 是2的倍数,则
是2的倍数,则![]() 一定是4的倍数”,这是三段论推理,但其结论是错误的.
一定是4的倍数”,这是三段论推理,但其结论是错误的.
②在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.
③由平面三角形的性质推测空间四面体的性质,这是一种合情推理.
④一个数列的前三项是1,2,3,那么这个数列的通项公式必为![]() .
.
A. ①③ B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一牧羊人赶着一群羊通过4个关口,每过一个关口,守关人将拿走当时羊的一半,然后退还一只给牧羊人,过完这些关口后,牧羊人只剩下3只羊,则牧羊人在过第1个关口前有_________只羊.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com