
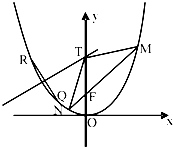
 如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.
如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.分析 (Ⅰ)由题意可设MN:y=kx+$\frac{p}{2}$,联立直线方程和抛物线方程,利用根与系数的关系结合x1x2=-4求得p值;
(Ⅱ)设R(x3,y3),Q(x4,y4),T(0,t),由T在RQ的垂直平分线上,列等式求得t的值,再由${S}_{△MNT}=\frac{1}{2}•|FT|•|{x}_{1}-{x}_{2}|=\frac{3}{4}|{x}_{1}-{x}_{2}|$,结合(Ⅰ)把面积转化为含有k的代数式求得最小值.
解答 解:(Ⅰ)由题意设MN:y=kx+$\frac{p}{2}$,
由$\left\{\begin{array}{l}{y=kx+\frac{p}{2}}\\{{x}^{2}=2py}\end{array}\right.$,消去y得,x2-2pkx-p2=0(*)
由题设,x1,x2是方程(*)的两实根,∴${x}_{1}{x}_{2}=-{p}^{2}=-4$,故p=2;
(Ⅱ)设R(x3,y3),Q(x4,y4),T(0,t),
∵T在RQ的垂直平分线上,∴|TR|=|TQ|.
得${{x}_{3}}^{2}+({y}_{3}-t)^{2}={{x}_{4}}^{2}+({y}_{4}-t)^{2}$,又${{x}_{3}}^{2}=4{y}_{3},{{x}_{4}}^{2}=4{y}_{4}$,
∴$4{y}_{3}+({y}_{3}-t)^{2}=4{y}_{4}+({y}_{4}-t)^{2}$,即4(y3-y4)=(y3+y4-2t)(y4-y3).
而y3≠y4,∴-4=y3+y4-2t.
又∵y3+y4=1,∴$t=\frac{5}{2}$,故T(0,$\frac{5}{2}$).
因此,${S}_{△MNT}=\frac{1}{2}•|FT|•|{x}_{1}-{x}_{2}|=\frac{3}{4}|{x}_{1}-{x}_{2}|$.
由(Ⅰ)得,x1+x2=4k,x1x2=-4,
${S}_{△MNT}=\frac{3}{4}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{3}{4}\sqrt{(4k)^{2}-4•(-4)}=3\sqrt{{k}^{2}+1}≥3$.
因此,当k=0时,S△MNT有最小值3.
点评 本题考查抛物线方程的求法,考查了直线和圆锥曲线间的关系,着重考查“舍而不求”的解题思想方法,考查了计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
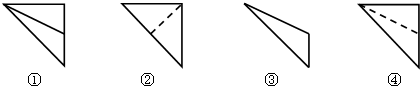
| A. | ①和③ | B. | ②和① | C. | ②和④ | D. | ④和③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com