
| A. | $\frac{1}{4030}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2}{2015}$ | D. | 0 |
分析 解法一:利用赋值法,x=1,x=0,然后求解就.
解法二:利用定积分直接求解即可.
解答 解法一:∵${(2x-1)^{2014}}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{2014}}{x^{2014}}$,
∴$\frac{1}{4030}{(2x-1)^{2015}}+C={a_0}x+\frac{1}{2}{a_1}{x^2}+\frac{1}{3}{a_2}{x^3}+…+\frac{1}{2015}{a_{2014}}{x^{2015}}$(C为常数),
取x=1得${a_0}+\frac{1}{2}{a_1}+\frac{1}{3}{a_2}+…+\frac{1}{2015}{a_{2014}}=\frac{1}{4030}+C$,
再取x=0得$\frac{1}{4030}{(-1)^{2015}}+C=0$,即得$C=\frac{1}{4030}$,
∴${a_0}+\frac{1}{2}{a_1}+\frac{1}{3}{a_2}+…+\frac{1}{2015}{a_{2014}}=\frac{1}{2015}$,
故选B.
解法二:∵${(2x-1)^{2014}}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{2014}}{x^{2014}}$,
∴${∫}_{0}^{1}{(2x-1)}^{2014}dx={∫}_{0}^{1}({a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}+…+{a}_{2014}{x}^{2014})dx$,
∴$\frac{1}{2015}={a_0}+\frac{1}{2}{a_1}+\frac{1}{3}{a_2}+…+\frac{1}{2015}{a_{2014}}$,
故选B.
点评 本题考查二项式定理的应用,定积分的求法,考查转化思想的应用.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
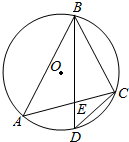 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
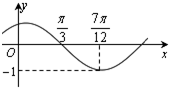 函数f(x)=Acos(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象.
函数f(x)=Acos(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
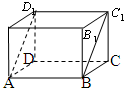 如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.
如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{127}{64}$ | B. | $\frac{511}{256}$ | C. | $\frac{1023}{512}$ | D. | $\frac{511}{512}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com