
分析 (1)若直线l的斜率不存在,则直线l:x=1,符合题意;若直线l的斜率存在,设直线l的方程为kx-y-k=0.由题意知,圆心(3,4)到已知直线l的距离等于半径2,由此利用点到直线的距离公式得$k=\frac{3}{4}$,从而求出直线的方程.
(2)设直线方程为kx-y-k=0,由弦长|PQ|求出弦心距$d=\sqrt{2}$,由此利用点到直线距离公式求出k=1或k=7,从而能求出直线l的方程.
解答 解:(1)若直线l的斜率不存在,则直线l:x=1,符合题意.
若直线l的斜率存在,设直线l的方程为y=k(x-1),即kx-y-k=0.
由题意知,圆心(3,4)到已知直线l的距离等于半径2,
即:$\frac{{|{3k-4-k}|}}{{\sqrt{{k^2}+1}}}=2$,解得$k=\frac{3}{4}$,此时直线的方程为3x-4y-3=0.
综上可得,所求直线l的方程是x=1或3x-4y-3=0.----(6分)
(2)直线与圆相交,斜率必定存在,且不为0,设直线方程为kx-y-k=0,
∵$|{PQ}|=2\sqrt{{r^2}-{d^2}}=2\sqrt{2}$,∴弦心距$d=\sqrt{2}$,即$\frac{{|{3k-4-k}|}}{{\sqrt{{k^2}+1}}}=2\sqrt{2}$,
解得k=1或k=7,
所求直线l的方程为x-y-1=0或7x-y-7=0.----(12分)
点评 本题考查直线方程的求法,考查直线方程、圆、点到直线的距离公式的应用等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
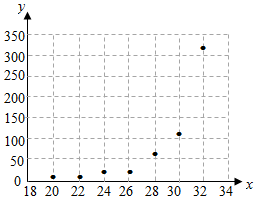 为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型①$y={C_1}{x^2}+{C_2}$与模型;②$y={e^{{C_3}x+{C_4}}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.
为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据列于下表中,并做出了散点图,发现样本点并没有分布在某个带状区域内,两个变量并不呈现线性相关关系,现分别用模型①$y={C_1}{x^2}+{C_2}$与模型;②$y={e^{{C_3}x+{C_4}}}$作为产卵数y和温度x的回归方程来建立两个变量之间的关系.| 温度x/°C | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline x$ | $\overline t$ | $\overline y$ | $\overline z$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{{\sum_{i=1}^7{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({x_i}-\overline x)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({t_i}-\overline t)({y_i}-\overline y)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({z_i}-\overline z)({x_i}-\overline x)}}}{{\sum_{i=1}^7{{{({x_i}-\overline x)}^2}}}}$ | $\frac{{\sum_{i=1}^7{({z_i}-\overline z)({t_i}-\overline t)}}}{{\sum_{i=1}^7{{{({t_i}-\overline t)}^2}}}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{10}$ | D. | $\frac{\sqrt{5}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≠$\frac{π}{4}$} | B. | {x|x≠$\frac{π}{4}$,k∈Z} | C. | {x|x≠kπ+$\frac{π}{4}$,k∈Z} | D. | {x|x≠$\frac{3π}{4}$+kπ,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com