
分析 根据函数成立的条件建立不等式关系即可得到结论.
解答 解:要使函数有意义,则1-tan2x≥0,
即tan2x≤1,
即kπ-$\frac{π}{2}$<2x≤kπ+$\frac{π}{4}$,k∈Z,
即$\frac{1}{2}$kπ-$\frac{π}{4}$<x≤$\frac{1}{2}$kπ+$\frac{π}{8}$,
即函数的定义域为($\frac{1}{2}$kπ-$\frac{π}{4}$,$\frac{1}{2}$kπ+$\frac{π}{8}$],k∈Z,
故答案为:($\frac{1}{2}$kπ-$\frac{π}{4}$,$\frac{1}{2}$kπ+$\frac{π}{8}$],k∈Z.
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
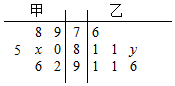 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值为2 | B. | 最小值为$\frac{5}{2}$ | C. | 最大值为2 | D. | 最大值为$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p:“?x0∈R,x02+x0+1<0”,则¬p:“?x∈R,x2+x+1≥0” | |
| B. | 命题“若x2-4x+3=0,则x=3”的逆否命题是假命题 | |
| C. | 命题“若m>0,则方程x2+x-m=0有实数根”的否定是“若m>0,则方程x2+x-m=0没有实数根” | |
| D. | 若p∧q为假命题,则p∨q为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com