
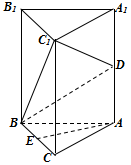
 如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.
如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.分析 (Ⅰ)设BC1的中点为F,连接EF,DF,则EF是△BCC1的中位线,证明:AE∥DF,即可证明直线AE∥平面BC1D;
(Ⅱ)利用等体积方法,求点E到平面BC1D的距离.
解答 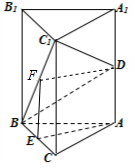 (Ⅰ)证明:设BC1的中点为F,连接EF,DF,则EF是△BCC1的中位线,
(Ⅰ)证明:设BC1的中点为F,连接EF,DF,则EF是△BCC1的中位线,
根据已知得EF∥DA,且EF=DA,(2分)
∴四边形ADFE是平行四边形,所以AE∥DF,
∵DF?平面BDC1,AE?平面BDC1
∴直线AE∥平面BDC1.(6分)
(Ⅱ)解:由(Ⅰ)的结论可知直线AE∥平面BDC1,
所以点E到平面BDC1的距离等于点A到平面BDC1的距离,设为h.
∴${V_{E-B{C_1}D}}={V_{A-B{C_1}D}}={V_{B-A{C_1}D}}$,(8分)
∴$\frac{1}{3}{S_{△B{C_1}D}}•h=\frac{1}{3}{S_{△A{C_1}D}}•\sqrt{3}$,(10分)
∴$\frac{1}{3}•\frac{1}{2}•2\sqrt{5}•\sqrt{3}•h=\frac{1}{3}•\frac{1}{2}•2•2•\sqrt{3}$,
所以解方程得,$h=\frac{{2\sqrt{5}}}{5}$.
所以点E到平面BDC1的距离为$\frac{{2\sqrt{5}}}{5}$.(12分)
点评 本题考查线面平行的判定,考查点到平面距离的计算,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
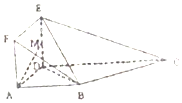 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
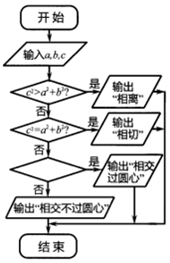 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )| A. | c=0? | B. | b=0? | C. | a=0? | D. | ab=0? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
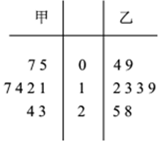 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
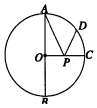 如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.
如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com