
| 3 |
| 1 |
| 3 |
| 2 |
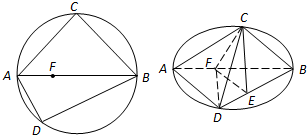
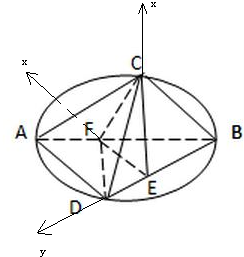
| 2 |
| 6 |
| 3 |
| 3 |
| BF |
| BA |
| BE |
| BD |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 6 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| AC |
| 3 |
| 3 |
| 2 |
| 2 |
| BD |
| AC |
| BD |
3
| ||||
3×
|
2
| ||
| 29 |
2
| ||
| 29 |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| a |
| f′(x) |
| 2x |
| 1 |
| 2 |
| 1 |
| 3•4k-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 现有一个寻宝游戏,规则如下:在起点P处有A、B、C三条封闭的单向线路,走完这三条线路所花费的时间分别为10分钟、20分钟、30分钟,游戏主办方将宝物放置在B线路上(参赛方并不知晓),开始寻宝时参赛方在起点处随机选择路线顺序,若没有寻到宝物,重新回到起点后,再从没有走过的线路中随机选择路线继续寻宝,直到寻到宝物并将其带回至P处,期间所花费的时间记为X.
现有一个寻宝游戏,规则如下:在起点P处有A、B、C三条封闭的单向线路,走完这三条线路所花费的时间分别为10分钟、20分钟、30分钟,游戏主办方将宝物放置在B线路上(参赛方并不知晓),开始寻宝时参赛方在起点处随机选择路线顺序,若没有寻到宝物,重新回到起点后,再从没有走过的线路中随机选择路线继续寻宝,直到寻到宝物并将其带回至P处,期间所花费的时间记为X.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com