
分析 化圆的方程为标准方程,求出圆心坐标和半径,设出OP所在直线斜率,由OP与圆相切求出k的范围,联立直线方程和椭圆方程,求出M的坐标,得到MA,MB的斜率,作积后求得答案.
解答 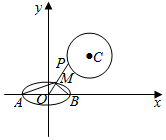 解:如图,
解:如图,
由圆C:x2+y2-8x-8y+28=0,得(x-4)2+(y-4)2=4,
由曲线N:x2+4y2=4,得$\frac{{x}^{2}}{4}+{y}^{2}=1$,
∴A(-2,0),B(2,0),
设k3=k,则OP方程为y=kx,
由C(4,4)到直线kx-y=0的距离d=$\frac{|4k-4|}{\sqrt{{k}^{2}+1}}=2$,
解得:$k=\frac{4-\sqrt{7}}{3}$或$k=\frac{4+\sqrt{7}}{3}$.
∴k的取值范围为[$\frac{4-\sqrt{7}}{3},\frac{4+\sqrt{7}}{3}$].
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,得M($\frac{2}{\sqrt{1+4{k}^{2}}},\frac{2k}{\sqrt{1+4{k}^{2}}}$)(不妨取M为第一象限的点),
则${k}_{1}=\frac{\frac{2k}{\sqrt{1+4{k}^{2}}}}{\frac{2}{\sqrt{1+4{k}^{2}}}+2}=\frac{k}{1+\sqrt{1+4{k}^{2}}}$,${k}_{2}=\frac{\frac{2k}{\sqrt{1+4{k}^{2}}}}{\frac{2}{\sqrt{1+4{k}^{2}}}-2}$=$\frac{k}{1-\sqrt{1+4{k}^{2}}}$,
∴k1•k2•k3 =$\frac{k}{1+\sqrt{1+4{k}^{2}}}•\frac{k}{1-\sqrt{1+4{k}^{2}}}•k$=$-\frac{k}{4}$.
∵k∈[$\frac{4-\sqrt{7}}{3},\frac{4+\sqrt{7}}{3}$],
∴k1•k2•k3 =$-\frac{k}{4}$∈[$-\frac{4+\sqrt{7}}{12},-\frac{4-\sqrt{7}}{12}$].
故答案为:[$-\frac{4+\sqrt{7}}{12},-\frac{4-\sqrt{7}}{12}$].
点评 本题考查椭圆的简单性质,考查了直线与圆,与圆锥曲线位置关系的应用,考查计算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,以下四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,以下四个命题:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点A(0,$\sqrt{3}$)和点P都在椭圆C1上,椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{{\sqrt{3}}}{3}})$ | B. | $({0,\frac{{\sqrt{3}}}{3}}]$ | C. | $({\frac{{\sqrt{3}}}{3},1})$ | D. | $[{\frac{{\sqrt{3}}}{3},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{2}-\frac{x^2}{8}=1$ | B. | $\frac{y^2}{8}-\frac{x^2}{2}=1$ | C. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com