
分析 (1)确定函数f(x)在[0,$\frac{π}{2}$]上单调递增,可得f(x)min=f(0)=-1;函数g(x)在[0,$\frac{π}{2}$]上单调递减,可得g(x)max=g(0)=-$\sqrt{2}$,即可求出实数m的范围;
(2)先利用分析要证原不等式成立,转化为只要证$\frac{{e}^{x}}{x+1}$>$\frac{cosx}{sinx+\sqrt{2}}$,令h(x)=$\frac{{e}^{x}}{x+1}$,x>-1,利用导数求出h(x)min=h(0)=1,再令k=$\frac{cosx}{sinx+\sqrt{2}}$,其可看作点A(sinx,cosx)与点B(-$\sqrt{2}$,0)连线的斜率,根据其几何意义求出k的最大值,即可证明.
解答 (1)解:∵f(x1)+g(x2)≥m,
∴f(x1)≥m-g(x2),
∴f(x1)min≥[m-g(x2)]min,
∴f(x1)min≥m-g(x2)max,
当x∈[0,$\frac{π}{2}$]时,f′(x)>0,函数f(x)在[0,$\frac{π}{2}$]上单调递增,
∴f(x)min≥f(0)=-1,
∵g(x)=xcosx-$\sqrt{2}$ex,
∴g′(x)=cosx-xsinx-$\sqrt{2}$ex,
∵x∈[0,$\frac{π}{2}$],
∴0≤cosx≤1,xsinx≥0,$\sqrt{2}$ex≥$\sqrt{2}$,
∴g′(x)≤0,
∴函数g(x)在[0,$\frac{π}{2}$]上单调递减,
∴g(x)max≥g(0)=-$\sqrt{2}$,
∴-1≥m+$\sqrt{2}$,
∴m≤-1-$\sqrt{2}$,
∴实数m的取值范围为(-∞,-1-$\sqrt{2}$];
(2)证明:x>-1,要证:f(x)-g(x)>0,
只要证f(x)>g(x),
只要证exsinx-cosx>xcosx-$\sqrt{2}$ex,
只要证ex(sinx+$\sqrt{2}$)>(x+1)cosx,
由于sinx+$\sqrt{2}$>0,x+1>0,
只要证$\frac{{e}^{x}}{x+1}>\frac{cosx}{sinx+\sqrt{2}}$,
下面证明x>-1时,不等式$\frac{{e}^{x}}{x+1}>\frac{cosx}{sinx+\sqrt{2}}$成立,
令h(x)=$\frac{{e}^{x}}{x+1}$,x>-1,
∴h′(x)=$\frac{x{e}^{x}}{(x+1)^{2}}$,x>-1,
当x∈(-1,0)时,h′(x)<0,h(x)单调递减,
当x∈(0,+∞)时,h′(x)>0,h(x)单调递增,
∴h(x)min=h(0)=1
令k=$\frac{cosx}{sinx+\sqrt{2}}$,其可看作点A(sinx,cosx)与点B(-$\sqrt{2}$,0)连线的斜率,
∴直线AB的方程为y=k(x+$\sqrt{2}$),
由于点A在圆x2+y2=1上,
∴直线AB与圆相交或相切,
当直线AB与圆相切且切点在第二象限时,直线AB的斜率取得最大值为1,
∴当x=0时,k=$\frac{\sqrt{2}}{2}$<1=h(0),x≠0时,h(x)>1≥k,
综上所述,当x>-1,f(x)-g(x)>0.
点评 本题考查了函数零点存在性定理,导数和函数的最值的关系,考查分类整合思想、转化思想,考查学生综合运用知识分析解决问题的能力,属于难题.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<2} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (1,5) | C. | (3,6) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
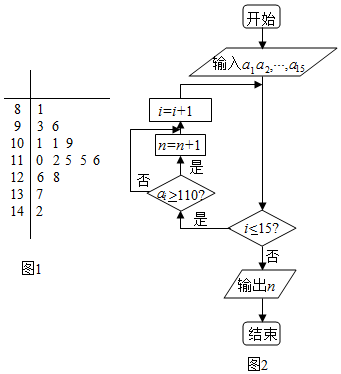 高三某班15名学生一次模拟考试成绩用茎叶图表示如图1,执行图2所示的程序框图,若输入的ai(i=1,2,…,15)分别为这15名学生的考试成绩,则输出的结果为( )
高三某班15名学生一次模拟考试成绩用茎叶图表示如图1,执行图2所示的程序框图,若输入的ai(i=1,2,…,15)分别为这15名学生的考试成绩,则输出的结果为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com