
【题目】如图,已知矩形![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为矩形内一点,且
为矩形内一点,且![]() ,设
,设![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.

【答案】(1)0;(2)2.
【解析】
(1)以A为坐标原点建立直角坐标系,分别求得A,B,C,D,P的坐标,运用向量数量积的坐标表示,计算可得结果;
(2)设P(cosα,sinα),分别求得向量![]() =(2﹣cosα,
=(2﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(﹣cosα,
=(﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(cosα,sinα),运用向量数量积的坐标表示,结合辅助角公式和正弦函数的图象和性质,即可得到所求最大值.
=(cosα,sinα),运用向量数量积的坐标表示,结合辅助角公式和正弦函数的图象和性质,即可得到所求最大值.
(1)如图,以A为坐标原点建立直角坐标系,
则A(0,0),B(2,0),C(2,![]() ),D(0,
),D(0,![]() ),
),
P(cos![]() ,sin
,sin![]() ),即(
),即(![]() ,
,![]() ),
),
![]()
![]() =(
=(![]() ,
,![]() )(﹣
)(﹣![]() ,
,![]() )=
)=![]() ×(﹣
×(﹣![]() )+(
)+(![]() )2=0;
)2=0;
(2)设P(cosα,sinα),
则![]() =(2﹣cosα,
=(2﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(﹣cosα,
=(﹣cosα,![]() ﹣sinα),
﹣sinα),![]() =(cosα,sinα),
=(cosα,sinα),
可得![]() +
+![]() =(2﹣2cosα,2
=(2﹣2cosα,2![]() ﹣2sinα),
﹣2sinα),
则(![]() +
+![]() )
)![]() =2cosα﹣2cos2α+2
=2cosα﹣2cos2α+2![]() sinα﹣2sin2α
sinα﹣2sin2α
=4(![]() sinα+
sinα+![]() cosα)﹣2=4sin(α+
cosα)﹣2=4sin(α+![]() )﹣2,
)﹣2,
当α+![]() =
=![]() ,即α=
,即α=![]() 时,
时,
(![]() )
)![]() 取得最大值4﹣2=2.
取得最大值4﹣2=2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,A1A=AB=6,D为AC中点.

(1)求三棱锥C1﹣BCD的体积;
(2)求证:平面BC1D⊥平面ACC1A1;
(3)求证:直线AB1∥平面BC1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
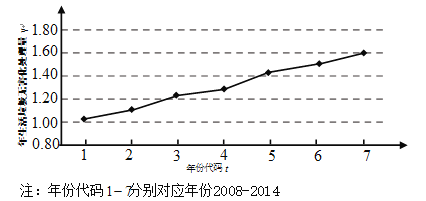
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请建立
的关系,请建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(2)预测2018年我国生活垃圾无害化处理量.
附注:
参考公式:设具有线性相关关系的两个变量![]() 的一组观察值为
的一组观察值为![]() ,
,
则回归直线方程![]() 的系数为:
的系数为:
 ,
, ![]() .
.
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某设备的使用年数x与所支出的维修总费用y的统计数据如下表:
使用年数x(单位:年) | 2 | 3 | 4 | 5 | 6 |
维修费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
根据上标可得回归直线方程为 ![]() =1.3x+
=1.3x+ ![]() ,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用年.
,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题有__________.
①回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数![]() 来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
来刻面回归效果;表示预报变量对解释变量变化的贡献率,越接近于1,说明模型的拟合效果越好;
④若分类变量![]() 和
和![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 越大,则“
越大,则“![]() 与
与![]() 相关”的可信程度越小;
相关”的可信程度越小;
⑤.对于自变量![]() 和因变量
和因变量![]() ,当
,当![]() 取值一定时,
取值一定时, ![]() 的取值具有一定的随机性,
的取值具有一定的随机性, ![]() ,
, ![]() 间的这种非确定关系叫做函数关系;
间的这种非确定关系叫做函数关系;
⑥.残差图中残差点比较均匀的地落在水平的带状区域中,说明选用的模型比较合适;
⑦.两个模型中残差平方和越小的模型拟合的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的方程为y=3+ ![]() .
.
(1)写出曲线C的一个参数方程;
(2)在曲线C上取一点P,过点P作x轴,y轴的垂线,垂足分别为A,B,求矩形OAPB的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点为
)的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为坐标原点.
为坐标原点.
(1)求抛物线![]() 的方程;
的方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com