
分析 (1)根据{an}为递增的等比数列且a32=a1a5,得到a1=1,a3=4,a5=16,进而求得an,bn的通项公式;
(2)利用裂项相消法求数列的前n项和,再用分离参数法和单调性求m的最小值.
解答 解:(1)因为数列{an}为递增的等比数列,且a32=a1a5,
再观察集合中的元素,只有42=1×16,
所以,a1=1,a3=4,a5=16,
所以,{an}的通项公式为:an=2n-1,
而bn+1-2bn=8an=2n+2,
所以,$\frac{{b}_{n+1}}{{2}^{n+1}}$-$\frac{{b}_{n}}{{2}^{n}}$=2,
所以,数列{$\frac{{b}_{n}}{{2}^{n}}$}是首项为1,公差为2的等差数列,
即$\frac{{b}_{n}}{{2}^{n}}$=2n-1,所以,bn=(2n-1)2n;
(2)因为cn=$\frac{{4}^{n}}{{b}_{n}•{b}_{n+1}}$=$\frac{4^n}{(2n-1)(2n+1)•{2}^{n}•{2}^{n+1}}$
=$\frac{1}{4}$[$\frac{1}{2n-1}-\frac{1}{2n+1}$],
所以,数列{cn}的前n项和为:Tn=$\frac{1}{4}$[1-$\frac{1}{2n+1}$],
根据题意,Tn>$\frac{1}{{a}_{m}}$可写成,$\frac{1}{4}$[1-$\frac{1}{2n+1}$]>$\frac{1}{{2}^{m-1}}$,
即2m-3>$\frac{1}{1-\frac{1}{2n+1}}$对任意正整数n都成立,设g(n)=$\frac{1}{1-\frac{1}{2n+1}}$,
显然,g(n)在自然数集上单调递减,
所以,2m-3>[g(n)]max=g(1)=$\frac{3}{2}$,即2m-2>3,
因此,满足上述不等式的m的最小整数为4,
故整数m的最小值为4.
点评 本题主要考查了数列通项公式的求法,涉及等差等比数列的性质,数列求和,以及与不等式的综合应用,属于难题.


科目:高中数学 来源: 题型:选择题
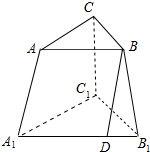 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )| A. | 平面 | B. | 直线 | ||
| C. | 线段,但只含1个端点 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-1,1] | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | . 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | .充要条件 | D. | . 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com