
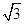 ,PD=CD=2.
,PD=CD=2.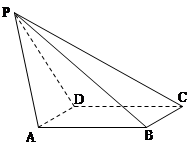
 是矩形,故
是矩形,故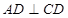 ,又由于
,又由于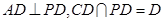 ,
,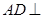 平面PDC,而
平面PDC,而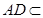 平面
平面 ,所以平面
,所以平面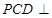 平面
平面 .
.
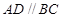 ,所以可知
,所以可知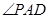 为异面直线
为异面直线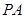 与
与 所成的角.
所成的角.
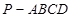 中,因为底面
中,因为底面 是矩形,
是矩形,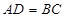 且
且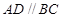 ,又因为
,又因为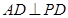 ,故
,故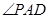 为异面直线
为异面直线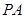 与
与 所成的角.
所成的角.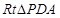 中,
中,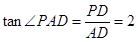 ,
,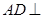 平面PDC即可.
平面PDC即可.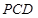 内,过点P作
内,过点P作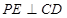 交直线CD于点E,连接EB.因为平面
交直线CD于点E,连接EB.因为平面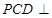 平面
平面 ,故
,故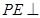 平面
平面 ,由此得
,由此得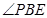 为直线PB与平面
为直线PB与平面 所成的角.余下的问题是解三角形求角.
所成的角.余下的问题是解三角形求角.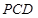 内,过点P作
内,过点P作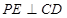 交直线CD于点E,连接EB.
交直线CD于点E,连接EB.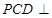 平面
平面 ,而直线CD是平面
,而直线CD是平面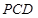 与平面
与平面 的交线,
的交线,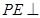 平面
平面 ,由此得
,由此得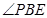 为直线PB与平面
为直线PB与平面 所成的角.
所成的角.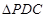 中,由于
中,由于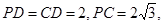 可得
可得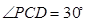 .
.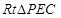 中,
中,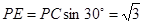 ,
,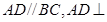 平面
平面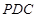 ,得
,得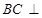 平面
平面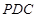 ,
,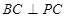 ,在
,在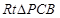 中,
中,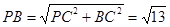 .
.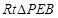 中,
中,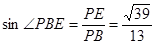
 .
.

科目:高中数学 来源:不详 题型:单选题
| A.直角三角形 | B.锐角三角形 | C.钝角三角形 | D.以上都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com