
分析 当点C位于垂直于面AOB的直径端点时,三棱锥O-ABC的体积最大,由此求出球O的半径,进而能求出球O的表面积.
解答 解:如图所示,当点C位于垂直于面AOB的直径端点时,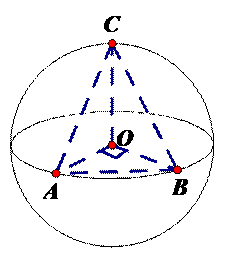
三棱锥O-ABC的体积最大,
设球O的半径为R,此时${V}_{O-ABC}={V}_{C-AOB}=\frac{1}{3}×\frac{1}{2}×{R}^{2}×R$=$\frac{9\sqrt{π}}{2{π}^{2}}$,
解得R=$\frac{3}{\sqrt{π}}$,
∴球O的表面积为S=4πR2=4π×$\frac{9}{π}$=36.
故答案为:36.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意球、三棱锥的性质及构造法的合理应用.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m∥n,n∥β,则 α⊥β | B. | 若α∥β,m?α,n?β,则 m∥n | ||
| C. | 若m⊥n,m?α,n?β,则α⊥β | D. | 若α⊥β,m?α,n?β,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
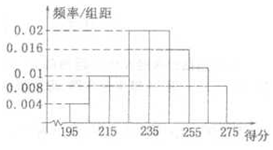 某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.
某高校组织自主招生考试,共有2 000名学生报名参加了笔试,成绩均介于195分到275分 之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275].如图是按上述分组方法得到的频率分布直方图,已知笔试成绩在260分以上(含260分)的同学取得面试资格.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
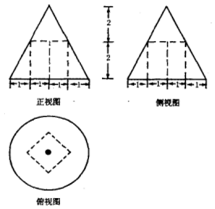
| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
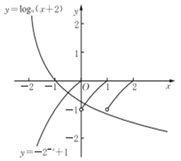 已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).
已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com