
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.

(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
![]() 根据已知条件动圆
根据已知条件动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切,即可得到其轨迹为椭圆,从而求出结果
外切,即可得到其轨迹为椭圆,从而求出结果
![]() 设
设![]() 的坐标是
的坐标是![]() ,切点
,切点![]() 坐标分别是
坐标分别是![]() ,
,![]() ,求出切线方程,继而得到经过
,求出切线方程,继而得到经过![]() 两点的直线
两点的直线![]() 的方程是
的方程是![]() ,讨论当
,讨论当![]() 时和当
时和当![]() 时
时![]() 的取值范围
的取值范围
(1)设动圆![]() 的半径为
的半径为![]() ,∵动圆
,∵动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切,
外切,
∴![]() ,且
,且![]() .
.
于是,![]() ,所以动圆圆心
,所以动圆圆心![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆.从而,
的椭圆.从而,![]() ,所以
,所以![]() .
.
故动圆圆心![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 上任意一点
上任意一点![]() 的坐标是
的坐标是![]() ,切点
,切点![]() 坐标分别是
坐标分别是![]() ,
,![]() ;则经过
;则经过![]() 点的切线斜率
点的切线斜率![]() ,方程是
,方程是![]() ,经过
,经过![]() 点的切线方程是
点的切线方程是![]() ,又两条切线
,又两条切线![]() ,
,![]() 相交于
相交于![]()
![]() .
.
则有![]() ,所以经过
,所以经过![]() 两点的直线
两点的直线![]() 的方程是
的方程是![]() ,
,
①当![]() 时,有
时,有![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ;
;
②当![]() 时,联立
时,联立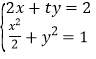 ,整理得
,整理得![]() ;
;
设![]() 坐标分别为
坐标分别为![]() ,
,![]() ,则
,则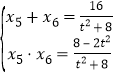 ,
,
所以![]() ,故
,故![]() ,
,
所以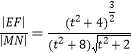 .令
.令![]() ,则
,则![]() ,则
,则![]() ,
,
又令![]() ,则
,则![]() ,
,![]() ,令
,令![]() ,
,
令![]() ,解可得
,解可得![]() ,故
,故![]() 在
在![]() 上单调递增,且有
上单调递增,且有![]() ,而
,而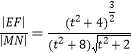 ,所以
,所以![]() ;
;
综合①,②可得![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】经销商第一年购买某工厂商品的单价为![]() (单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
(单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
上一年度 销售额/万元 |
|
|
|
|
|
|
商品单价/元 |
|
|
|
|
|
|
为了研究该商品购买单价的情况,为此调查并整理了![]() 个经销商一年的销售额,得到下面的柱状图.
个经销商一年的销售额,得到下面的柱状图.
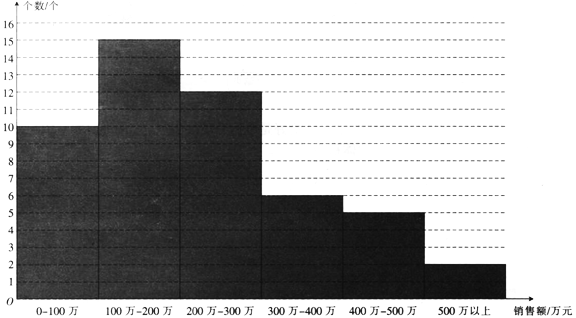
已知某经销商下一年购买该商品的单价为![]() (单位:元),且以经销商在各段销售额的频率作为概率.
(单位:元),且以经销商在各段销售额的频率作为概率.
(1)求![]() 的平均估计值.
的平均估计值.
(2)为了鼓励经销商提高销售额,计划确定一个合理的年度销售额![]() (单位:万元),年销售额超过
(单位:万元),年销售额超过![]() 的可以获得红包奖励,该工厂希望使
的可以获得红包奖励,该工厂希望使![]() 的经销商获得红包,估计
的经销商获得红包,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝中国人民解放军建军90周年,南昌市某校打算组织高一6个班级参加红色旅游活动,旅游点选取了八一南昌起义纪念馆,南昌新四军军部旧址等5个红色旅游景点.若规定每个班级必须参加且只能游览1个景点,每个景点至多有两个班级游览,则这6个班级中没有班级游览新四军军部旧址的不同游览方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c的图象与x轴有两个不同的交点,若f(c)=0且0<x<c时,f(x)>0,
(1)证明:![]() 是f(x)=0的一个根;
是f(x)=0的一个根;
(2)试比较![]() 与c的大小;
与c的大小;
(3)证明:-2<b<-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|x2-8x-20≤0},S={x||x-1|≤m}.
(1)若(P∪S)P,求实数m的取值范围;
(2)是否存在实数m,使得“x∈P”是“x∈S”的充要条件?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logax,
(1)若y=f(x)+b的定义域和值域都是[1,3],求a,b的值;
(2)当a>1时,若![]() 在
在![]() 上恒成立,则m的取值范围.
上恒成立,则m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com