
| A. | $\frac{1}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
分析 由已知及诱导公式可得cos($\frac{3π}{10}$+θ)=$\frac{\sqrt{6}}{3}$,利用诱导公式,二倍角的余弦函数公式化简所求,即可化简计算求值.
解答 解:∵sin($\frac{π}{5}$-θ)=$\frac{\sqrt{6}}{3}$,
⇒cos[$\frac{π}{2}$-($\frac{π}{5}$-θ)]=cos($\frac{3π}{10}$+θ)=$\frac{\sqrt{6}}{3}$,
∴sin($\frac{11π}{10}$+2θ)=sin[$\frac{π}{2}$+($\frac{3π}{5}$+2θ)]=cos($\frac{3π}{5}$+2θ)=2cos2($\frac{3π}{10}$+θ)-1=2×($\frac{\sqrt{6}}{3}$)2-1=$\frac{1}{3}$.
故选:A.
点评 本题主要考查了诱导公式,二倍角的余弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于中档题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 在医院调查了1000名老年人的健康状况 | |
| C. | 调查了10名老年邻居的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
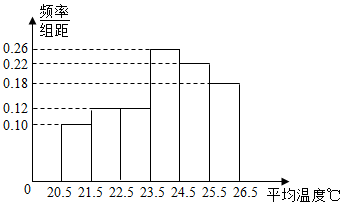
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sin2x | B. | f(x)=2tan$\frac{1}{2}$x | C. | f(x)=-tanx | D. | f(x)=sin($\frac{π}{2}$+2x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t为任意实数,{an}均是等比数列 | B. | 当且仅当t=-1时,{an}是等比数列 | ||
| C. | 当且仅当t=0时,{an}是等比数列 | D. | 当且仅当t=-2时,{an}是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只有一条,但不一定在平面β内 | B. | 只有一条,一定在平面β内 | ||
| C. | 有无数条,但都不在平面β内 | D. | 有无数条,都在平面β内 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com