
分析 令f(x)=t,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数问题?f(t)-2t-$\frac{3}{2}$=0的根的个数问题.结合图象可得f(t)-2t-$\frac{3}{2}$=0的根t1<0,t2∈(1,2).f(x)=t1无解,f(x)=t2有3解,解得得到函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数
解答  解:令f(x)=t,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数问题?f(t)-2t-$\frac{3}{2}$=0的根的个数问题.
解:令f(x)=t,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数问题?f(t)-2t-$\frac{3}{2}$=0的根的个数问题.
即y=f(t),y=2t+$\frac{3}{2}$的图象如图(1),结合图象可得f(t)-2t-$\frac{3}{2}$=0的根t1<0,t2∈(1,2).
f(x)=t1无解,f(x)=t2有3解,
综上,函数F(x)=f[f(x)]-2f(x)-$\frac{3}{2}$的零点个数是3.
故答案为:3
点评 本题考查了复合函数零点问题,解题的关键是合理利用换元思想求解,属于中档题.


科目:高中数学 来源: 题型:解答题
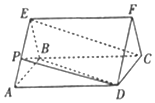 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线 | B. | 椭圆 | C. | 圆 | D. | 直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,1) | B. | (1,+∞) | C. | ($\frac{2}{3}$,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com