
分析 (1)分别求得A1P与A2Q的方程,两式相乘,化简整理即可求得动点M的轨迹D的方程;
(2)当直线斜率存在时,设直线方程,代入椭圆方程,利益韦达定理及向量数量积的坐标运算,即可求得实数λ的取值范围.
解答 解:(1)由已知A1(-2,0),A2(2,0),设$P({t,\frac{{\sqrt{{t^2}-4}}}{2}}).Q({t,-\frac{{\sqrt{{t^2}-4}}}{2}})$
则直线${A_1}P:y=\frac{{\sqrt{{t^2}-4}}}{{2({t+2})}}({x+2})$,
直线${A_2}Q:y=\frac{{-\sqrt{{t^2}-4}}}{{2({t-2})}}({x-2})$,
两式相乘得${y^2}=\frac{-1}{4}({{x^2}-4})$,化简得$\frac{x^2}{4}+{y^2}=1$,
即动点M的轨迹D的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)过E(0,2)的直线若斜率不存在则$λ=\frac{1}{3}$或3,
设直线斜率k存在,A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}y=kx+2\\{x^2}+4{y^2}-4=0\end{array}\right.⇒({1+4{k^2}}){x^2}+16kx+12=0$,
则$\left\{\begin{array}{l}△≥0(1)\\{x_1}+{x_2}=-\frac{16k}{{1+4{k^2}}}(2)\\{x_1}{x_2}=\frac{12}{{1+4{k^2}}}(3)\\{x_1}=λ{x_2}(4)\end{array}\right.$
由(2)(4)解得x1,x2代入(3)式得$\frac{λ}{{{{({1+λ})}^2}}}•{({\frac{-16k}{{1+4{k^2}}}})^2}=\frac{12}{{1+4{k^2}}}$,
化简得$\frac{λ}{{{{({1+λ})}^2}}}=\frac{3}{64}({\frac{1}{k^2}+4})$,
由(1)△≥0解得${k^2}≥\frac{3}{4}$代入上式右端得,$\frac{3}{16}<\frac{λ}{{{{({1+λ})}^2}}}≤\frac{1}{4}$,
解得$\frac{1}{3}<λ<3$,
综上实数的取值范围是$[{\frac{1}{3},3}]$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2-i | B. | 2+3i | C. | $\frac{1}{2}$-i | D. | $\frac{1}{2}+i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
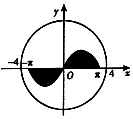 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com