Question

【题目】已知函数 的部分图象如图所示．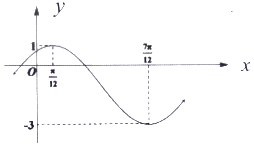
（1）求f（x）的解析式；
（2）求f（x）的单调递增区间和对称中心坐标；
（3）将f（x）的图象向左平移 个单位，再讲横坐标伸长到原来的2倍，纵坐标不变，最后将图象向上平移1个单位，得到函数g（x）的图象，求函数y=g（x）在 上的最大值和最小值．

Answer 1

【答案】
（1）解：由图象可知 ，可得：A=2，B=﹣1，

又由于 = ﹣ ，可得：T=π，所以 ，

由图象及五点法作图可知：2× +φ= ，所以φ= ，

所以f（x）=2sin（2x+ ）﹣1

（2）解：由（1）知，f（x）=2sin（2x+ ）﹣1，

令2kπ﹣ ≤2x+ ≤2kπ+ ，k∈Z，

得kπ﹣ ≤x≤kπ+ ，k∈Z，

所以f（x）的单调递增区间为[kπ﹣ ，kπ+ ]，k∈Z，

令2x+ =kπ，k∈Z，得x= ﹣ ，k∈Z，

所以f（x）的对称中心的坐标为（ ﹣ ，﹣1），k∈Z

（3）解：由已知的图象变换过程可得：g（x）=2sin（x+ ），

因为0≤x≤ ，所以 ≤ ，

所以当x+ = ，得x= 时，g（x）取得最小值g（ ）=﹣2，

当x+ = ，即x=0时，g（x）取得最大值g（0）=

【解析】（1）由图象可求A，B，T，利用周期公式可得 ，由图象及五点法作图可求φ，即可得解f（x）的函数解析式．（2）令2kπ﹣ ≤2x+ ≤2kπ+ ，k∈Z，解得kπ﹣ ≤x≤kπ+ ，k∈Z，可得f（x）的单调递增区间，令2x+ =kπ，k∈Z，可求f（x）的对称中心的坐标．（3）由已知的图象变换过程可得：g（x）=2sin（x+ ），结合范围0≤x≤ ，可求 ≤ ，利用正弦函数的图象和性质即可计算得解．
【考点精析】解答此题的关键在于理解三角函数的最值的相关知识，掌握函数，当时，取得最小值为；当时，取得最大值为，则，，．