
分析 (1)利用基本不等式即可证明.
(2)用分析法证.欲证要证证:$\sqrt{{b}^{2}-ac}$<$\sqrt{3}$a,平方后寻求使之成立的充分条件即可.
解答 证明:(1)a,b,c均为正实数,a+b+c=1,
$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=$\frac{a+b+c}{c}$+$\frac{a+b+c}{b}$+$\frac{a+b+c}{a}$
=3+($\frac{b}{a}$+$\frac{a}{b}$)+($\frac{c}{a}$+$\frac{a}{c}$)+($\frac{b}{c}$+$\frac{c}{b}$)≥3+2+2+2=9,当且仅当a=b=c=$\frac{1}{3}$时取等号,
故:$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≥9;
(2)要证:$\sqrt{{b}^{2}-ac}$<$\sqrt{3}$a.
只需证b2-ac<3a2,
∵a+b+c=0
即证b2+a(a+b)<3a2,即证(a-b)(2a+b)>0,
即证(a-b)(a-c)>0.
∵a>b>c,
∴a-b>0,a-c>0
∴(a-b)•(a-c)>0成立.
∴原不等式成立.
点评 本题考查了基本不等式的应用和分析法证明不等式,当用综合法不易发现解题途径时,我们可以从求证的不等式出发,逐步分析寻求使这个不等式成立的充分条件,直至所需条件为已知条件或一个明显成立的事实,从而得出要证的不等式成立,这种执果所因的思考和证明方法叫做分析法.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,4) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
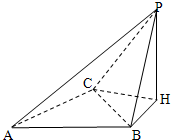 如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16\sqrt{2}}{3}$cm3 | B. | $\frac{32}{3}$cm3 | C. | 16$\sqrt{2}$cm3 | D. | 32cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
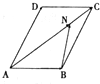
| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com