
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
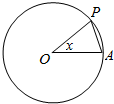 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )| A. | 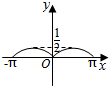 | B. | 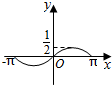 | C. |  | D. | 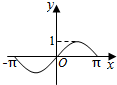 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 传染病医院感染禽流感的医务人员数与医院收治的禽流感病人数是具有相关关系的两个变量 | |
| B. | 从参加高三模拟考试的1200名学生中,随机抽取100人了解试卷难易情况可以用系统抽样 | |
| C. | 回归直线$\widehat{y}$=bx+a必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| D. | 对一组数据进行适当整理后,众数所在的一组频数最大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com