
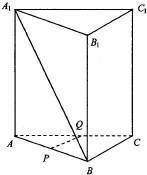
 如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.
如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.分析 (Ⅰ)根据条件即可得到PQ∥BC,从而由线面平行的判定定理得出直线PQ∥平面B1BCC1;
(Ⅱ)连接BQ,A1Q,根据已知条件即可说明∠BA1Q便是直线A1B和平面ACC1A1所成角,根据已知的边的长度求出BQ,A1B,从而在Rt△A1BQ中,由sin∠BA1Q=$\frac{BQ}{{A}_{1}B}$即可求得答案.
解答 解:(Ⅰ)证明:∵点P,Q分别是AB,AC的中点;
∴PQ∥BC,BC?平面B1BCC1,PQ?平面B1BCC1;
∴直线PQ∥平面B1BCC1;
(Ⅱ)如图,连接BQ,QA1;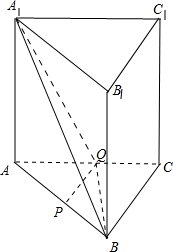 ∵三棱柱ABC-A1B1C1的侧棱和底面垂直;
∵三棱柱ABC-A1B1C1的侧棱和底面垂直;
∴A1A⊥平面ABC,BQ?平面ABC;
∴A1A⊥BQ,即BQ⊥A1A;
又△ABC三边相等,Q为AC中点;
∴BQ⊥AC,A1A∩AC=A;
∴BQ⊥平面ACC1A1;
∴∠BA1Q是直线A1B和平面ACC1A1所成的角;
∵AB=BC=AC=A1A=2;
∴$BQ=\sqrt{3}$,${A}_{1}B=2\sqrt{2}$;
∴在Rt△A1BQ中,sin∠BA1Q=$\frac{BQ}{{A}_{1}B}=\frac{\sqrt{3}}{2\sqrt{2}}=\frac{\sqrt{6}}{4}$;
∴直线A1B与平面ACC1A1所成角的正弦值为$\frac{\sqrt{6}}{4}$.
点评 考查三角形中位线的性质,线面平行的判定定理,以及线面垂直的性质,线面垂直的判定定理,线面角的概念及找法,正弦函数的定义.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
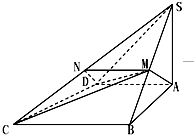 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x=k•180°,k∈Z} | B. | {x|x=k•180°+90°,k∈Z} | ||
| C. | {x|x=k•360°,k∈Z} | D. | {x|x=k•360°+90°,k∈Z} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com