从A.B.C.D.E5名学生中选出4名分别参加数学.物理.化学.外语竞赛.其中A不参加物理.化学竞赛.则不同的参赛方案种数为( )A．24B．48C．72D．120 题目和参考答案——青夏教育精英家教网—

20．从A，B，C，D，E5名学生中选出4名分别参加数学、物理、化学、外语竞赛，其中A不参加物理、化学竞赛，则不同的参赛方案种数为（　　）

A．

B．

C．

D．

120

分析根据题意，分2种情况讨论：①、A不参加任何竞赛，此时只需要将B、C、D、E四个人全排列，对应参加四科竞赛即可，由排列公式可得此时参赛方案的种数，②、A参加竞赛，依次分析A与其他四人的情况数目，由分步计数原理可得此时参赛方案的种数；进而由分类计数原理计算可得答案．

解答解：根据题意，分2种情况讨论：
①、A不参加任何竞赛，
此时只需要将B、C、D、E四个人全排列，对应参加四科竞赛即可，有A₄⁴=24种参赛方案；
②、A参加竞赛，
此时A只能参加数学和外语竞赛，有2种情况，
在剩下的4人中任选3人，参加其他三科的竞赛，有A₄³=24种情况，
此时共有2×24=48种参赛方案；
综上，一共有24+48=72种参赛方案；
故选：C．

点评本题考查排列组合的应用，此类问题一般优先分析“特殊”元素，即受到限制的元素．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

10．在△ABC中，$\overrightarrow{AB}$=$\overrightarrow{c}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，若点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$，则$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$（用向量$\overrightarrow{b}$、$\overrightarrow{c}$表示）．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．

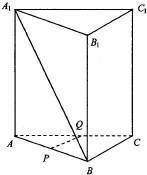如图，侧棱与底面积垂直的三棱柱ABC-A₁B₁C₁各侧棱和底面边长均为2，P，Q分别是棱AB、AC的中点，连结A₁B．
（Ⅰ）求证：直线PQ∥平面B₁BCC₁；
（Ⅱ）求直线A₁B与平面ACC₁A₁所成角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．已知等差数列{a_n}的前n项和S_n满足S₃=6，S₅=$\frac{25}{2}$．
（Ⅰ）求{a_n}的通项公式；
（II）求数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．已知$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$是向量，给出下列命题：
①若$\overrightarrow{a}$=$\overrightarrow{b}$，$\overrightarrow{b}$=$\overrightarrow{c}$，则$\overrightarrow{a}$=$\overrightarrow{c}$ ②若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$
③若$\overrightarrow{a}$=$\overrightarrow{b}$，则$\overrightarrow{a}$∥$\overrightarrow{b}$ ④若$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$=$\overrightarrow{b}$
⑤若|$\overrightarrow{a}$|≠|$\overrightarrow{b}$|，则$\overrightarrow{a}$＞$\overrightarrow{b}$或$\overrightarrow{a}$＜$\overrightarrow{b}$，
其中正确命题的序号是①③．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．房山区某高中为了推进新课程改革，满足学生全面发展的需求，决定从高一年级开始，在每周的周一、周三、周五的格外活动期间同时开设信息技术、美术素描和音乐欣赏辅导讲座，每位同学可以在期间的任何一天参加任何一门科目的辅导讲座，也可以放弃任何一门科目的辅导讲座．（规定：各科达到预先设定的人数时称为满座，否则称为不满座）统计数据表明，各学科讲座各天的满座的概率如下表：

	信息技术	美术素描	音乐欣赏
周一	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{2}$
周三	$\frac{1}{2}$	$\frac{1}{2}$	$\frac{2}{3}$
周五	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{2}{3}$