
| 信息技术 | 美术素描 | 音乐欣赏 | |
| 周一 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 周三 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 周五 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
分析 (1)设数学辅导讲座在周一、周三、周五都不满座为事件A,利用对立事件和独立事件同时发生的概率计算公式能够求出数学辅导讲座在周一、周三、周五都不满座的概率.
(2)X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
解答 解:(1)设数学辅导讲座在周一、周三、周五都不满座为事件A,
则P(A)=(1-$\frac{1}{2}$)×(1-$\frac{2}{3}$)×(1-$\frac{2}{3}$)=$\frac{1}{18}$.
(2)X的可能取值为0,1,2,3,
P(X=0)=(1-$\frac{1}{2}$)×(1-$\frac{1}{2}$)×(1-$\frac{2}{3}$)=$\frac{1}{12}$,
P(X=1)=$\frac{1}{2}$×(1-$\frac{1}{2}$)×(1-$\frac{2}{3}$)+(1-$\frac{1}{2}$)×$\frac{1}{2}$×(1-$\frac{2}{3}$)+(1-$\frac{1}{2}$)×(1-$\frac{1}{2}$)×$\frac{2}{3}$=$\frac{1}{3}$,
P(X=2)=$\frac{1}{2}$×$\frac{1}{2}$×(1-$\frac{2}{3}$)+(1-$\frac{1}{2}$)×$\frac{1}{2}$×$\frac{2}{3}$+$\frac{1}{2}$×(1-$\frac{1}{2}$)×$\frac{2}{3}$=$\frac{5}{12}$,
P(X=3)=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{2}{3}$=$\frac{1}{6}$,
∴随机变量X的分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{1}{3}$ | $\frac{5}{12}$ | $\frac{1}{6}$ |
点评 本题考查离散随机变量的概率分布列和数学期望,是历年高考的必考题型之一.解题时要认真审题,注意排列组合知识和概率知识的灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
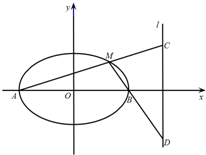 已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.
已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com