
分析 (1)根据题意,利用韦达定理列出关系式,利用完全平方公式及同角三角函数间的基本关系化简求出b的值即可;
(2)由b的值,利用完全平方公式求出sinθ与cosθ的值,原式通分并利用同角三角函数间的基本关系化简,将sinθ与cosθ的值代入计算即可求出值.
解答 解:(1)∵169x2-bx+60=0的两根为sinθ、cosθ,
∴sinθ+cosθ=$\frac{b}{169}$,sinθcosθ=$\frac{60}{169}$>0,
∵$θ∈({\frac{π}{4}\;,\;\;\frac{3π}{4}})$,
∴θ+$\frac{π}{4}$∈($\frac{π}{2}$,π),即sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$)>0,
∴(sinθ+cosθ)2=sin2θ+cos2θ+2sinθcosθ=1+2×$\frac{60}{169}$=($\frac{b}{169}$)2,
解得:b=±221(负值舍去),则b=221;
(2)∵(sinθ-cosθ)2=sin2θ+cos2θ-2sinθcosθ=1-2×$\frac{60}{169}$=$\frac{49}{169}$,
∴sinθ-cosθ=$\frac{7}{13}$,
∵sinθ+cosθ=$\frac{17}{13}$,
∴sinθ=$\frac{12}{13}$,cosθ=$\frac{5}{13}$,
则原式=$\frac{si{n}^{2}θ+1-co{s}^{2}θ}{sinθ(1-cosθ)}$=$\frac{2sinθ}{1-cosθ}$=3.
点评 此题考查了同角三角函数间基本关系的运用,以及完全平方公式的运用,熟练掌握基本关系是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
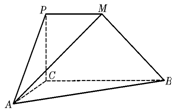 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=AC=1,BC=2,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=AC=1,BC=2,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |r|≤1;r越大,相关程度越大;反之,相关程度越小 | |
| B. | 线性回归方程对应的直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$至少经过其样本数据点(x1,y1),(x2,y2),(x3,y3),(xn,yn)中的一个点 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,相关指数R2为0.98的模型比相关指数R2为0.80的模型拟合的效果差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com