
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= ![]() .
.
(Ⅰ)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(Ⅱ)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
【答案】解:(Ⅰ)∵c=2,C= ![]() ,c2=a2+b2﹣2abcosC
,c2=a2+b2﹣2abcosC
∴a2+b2﹣ab=4,
又∵△ABC的面积等于 ![]() ,
,
∴ ![]() ,
,
∴ab=4
联立方程组 ![]() ,解得a=2,b=2
,解得a=2,b=2
(Ⅱ)∵sinC+sin(B﹣A)=sin(B+A)+sin(B﹣A)=2sin2A=4sinAcosA,
∴sinBcosA=2sinAcosA
当cosA=0时, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求得此时
,求得此时 ![]()
当cosA≠0时,得sinB=2sinA,由正弦定理得b=2a,
联立方程组 ![]() 解得
解得 ![]() ,
, ![]() .
.
所以△ABC的面积 ![]()
综上知△ABC的面积 ![]()
【解析】(Ⅰ)先通过余弦定理求出a,b的关系式;再通过正弦定理及三角形的面积求出a,b的另一关系式,最后联立方程求出a,b的值.(Ⅱ)通过C=π﹣(A+B)及二倍角公式及sinC+sin(B﹣A)=2sin2A,求出∴sinBcosA=2sinAcosA.当cosA=0时求出a,b的值进而通过 ![]() absinC求出三角形的面积;当cosA≠0时,由正弦定理得b=2a,联立方程解得a,b的值进而通过
absinC求出三角形的面积;当cosA≠0时,由正弦定理得b=2a,联立方程解得a,b的值进而通过 ![]() absinC求出三角形的面积.
absinC求出三角形的面积.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】长郡中学学习兴趣小组通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:

(1)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深层采访,求这3名学生中至少有2名要挑同桌的概率;
(2)根据以上![]() 列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?下面的临界值表仅供参考:
列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?下面的临界值表仅供参考:

(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差 | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 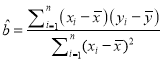 ,
, ![]() ,
,
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}满足:a1=1且a2 , a5 , a14成等比数列.
(1)求数列{an}的通项公式an和前n项和Sn;
(2)证明不等式 ![]() 且n∈N*)
且n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆心角为直角的扇形![]() 花草房,半径为1,点
花草房,半径为1,点![]() 是花草房弧上一个动点,不含端点,现打算在扇形
是花草房弧上一个动点,不含端点,现打算在扇形![]() 内种花,
内种花, ![]() ,垂足为
,垂足为![]() ,
, ![]() 将扇形
将扇形![]() 分成左右两部分,在
分成左右两部分,在![]() 左侧部分三角形
左侧部分三角形![]() 为观赏区,在
为观赏区,在![]() 右侧部分种草,已知种花的单位面积的造价为
右侧部分种草,已知种花的单位面积的造价为![]() ,种草的单位面积的造价为2
,种草的单位面积的造价为2![]() ,其中
,其中![]() 为正常数,设
为正常数,设![]() ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,总造价为
,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,总造价为![]()

求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
求当![]() 为何值时,总造价最小,并求出最小值。
为何值时,总造价最小,并求出最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,离心率 ![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若经过左焦点F1且倾斜角为 ![]() 的直线l与椭圆交于A、B两点,求|AB|的值.
的直线l与椭圆交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间几何体A﹣BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点. (Ⅰ)求证:BF∥平面ADE;
(Ⅱ)若AC=4,求证:平面ADE⊥平面BCDE;
(Ⅲ)若AC=4,求几何体C﹣BDF的体积.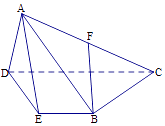
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com