
【题目】已知函数f(x)=x2+px+q与函数y=f(f(f(x)))有一个相同的零点,则f(0)与f(1)( )
A.均为正值
B.均为负值
C.一正一负
D.至少有一个等于0
【答案】D
【解析】解:设m是函数f(x)=x2+px+q与函数y=f(f(f(x)))的一个相同的零点, 则 f(m)=0,且f(f(f(m)))=0.
故有 f(f(m))=f(0)=q,且f(f(f(m)))=f(q)=q2+pq+q=q(q+p+1)=0,
即f(0)f(1)=0,故 f(0)与f(1)至少有一个等于0.
故选D.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减,以及对函数的零点的理解,了解函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.
上递减,以及对函数的零点的理解,了解函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且当倾斜角为
两点,且当倾斜角为![]() 的直线
的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() 时,有
时,有![]() .
.
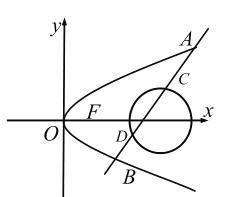
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆![]() ,是否存在倾斜角不为
,是否存在倾斜角不为![]() 的直线
的直线![]() ,使得线段
,使得线段![]() 被圆
被圆![]() 截成三等分?若存在,求出直线
截成三等分?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,抛物线
,抛物线![]() 的焦点在
的焦点在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点,点
的顶点均为原点,点 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,
(1)求曲线![]() ,
, ![]() 的标准方程;
的标准方程;
(2)请问是否存在过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,使得以线段
,使得以线段![]() 为直径的圆过原点
为直径的圆过原点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级随机抽取了![]() 名学生第一学期的数学学期综合成绩和物理学期综合成绩.
名学生第一学期的数学学期综合成绩和物理学期综合成绩.
列表如下:
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
学生序号 |
|
|
|
|
|
|
|
|
|
|
数学学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
物理学期综合成绩 |
|
|
|
|
|
|
|
|
|
|
规定:综合成绩不低于![]() 分者为优秀,低于
分者为优秀,低于![]() 分为不优秀.
分为不优秀.
对优秀赋分![]() ,对不优秀赋分
,对不优秀赋分![]() ,从
,从![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生,若用
名学生,若用![]() 表示这
表示这![]() 名学生两科赋分的和,求
名学生两科赋分的和,求![]() 的分布列和数学期望;
的分布列和数学期望;
根据这次抽查数据,列出![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为物理成绩与数学成绩有关?
的前提下认为物理成绩与数学成绩有关?
附:  ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆![]() 的周长和面积同时等分成两部分的函数称为圆
的周长和面积同时等分成两部分的函数称为圆![]() 的一个“太极函数”.下列有关说法中:
的一个“太极函数”.下列有关说法中:

①对圆![]() 的所有非常数函数的太极函数中,一定不能为偶函数;
的所有非常数函数的太极函数中,一定不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的太极函数;
的太极函数;
④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数.
的太极函数.
所有正确说法的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
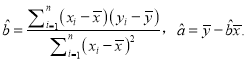
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com