
| A. | 若“p∧(?q)”为真命题,则“p∧q”也为真命题 | |
| B. | “x=3”是“2x2-7x+3=0”成立的充分不必要条件 | |
| C. | 命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0” | |
| D. | 线性回归方程$\hat y=\hat bx+\hat a$对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点 |
分析 利用复合命题的真假判断A的正误;充要条件判断B的正误;命题的否定判断C的正误;回归直线方程的性质判断D的正误.
解答 解:对于A,若“p∧(?q)”为真命题,说明P与?q是真命题,则“p∧q”也为真命题是错误的.
对于B,x=3可得“2x2-7x+3=0”成立,但是2x2-7x+3=0可得x=3或x=$\frac{1}{2}$,所以B的判断不正确;
对于C,命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0”,不满足命题的否定的定义,所以不正确;
对于D,线性回归方程$\hat y=\hat bx+\hat a$对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点,显然不满足回归直线方程的性质,所以不正确;
故选:B.
点评 本题考查命题的真假的判断与应用,充要条件,命题的否定,回归直线方程,复合命题的真假的判断,难度不大,但是考查知识全面.


科目:高中数学 来源: 题型:解答题
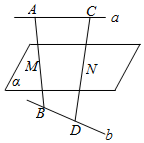 如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.
如图,a,b是异面直线,A,C与B,D分别是a,b上的两点,直线a∥平面α,直线b∥平面α,AB∩α=M,CD∩α=N,若AM=BM,求证:CN=DN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
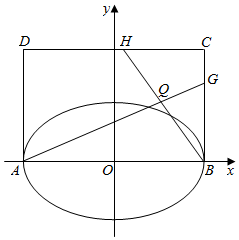 如图,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点,四边形ABCD为矩形,且AD=2b,H、G分别在线段DC、BC上,BH与AG相交于Q,且$\overrightarrow{BG}=λ\overrightarrow{BC}$,$\overrightarrow{CH}=μ\overrightarrow{CD}$.
如图,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴端点,四边形ABCD为矩形,且AD=2b,H、G分别在线段DC、BC上,BH与AG相交于Q,且$\overrightarrow{BG}=λ\overrightarrow{BC}$,$\overrightarrow{CH}=μ\overrightarrow{CD}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com