练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．在棱长为3的正方体内任取一个点，则这个点到各面的距离都大于1的概率为$\frac{1}{27}$．

    分析 求得满足条件的几何体的体积，利用体积比求概率．

    解答 解：在正方体内，到各面的距离大于1的点位于一个边长为1的小正方体内，
    小正方体的体积为1，
    大正方体的体积为33=27，
    ∴所求概率为$\frac{1}{27}$．
    故答案为：$\frac{1}{27}$．

    点评 本题考查了几何概型的概率计算，利用体积比求概率是几何概型概率计算的常用方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．若直线l与两直线y=1，直线x-y-7=0分别交于M，N两点且MN的中点为P（1，-1），则直线l的斜率等于（　　）
    A．$\frac{2}{3}$B．-$\frac{2}{3}$C．$\frac{3}{2}$D．-$\frac{3}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在△ABC中，a2+b2+c2=2$\sqrt{3}$bcsinA，则△ABC的形状是（　　）
    A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

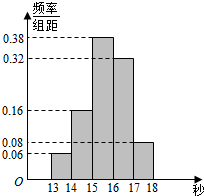    8．某班50名学生在一次百米测试中，成绩全部在13秒与18秒之间，大于或等于14秒的为良好，由测试结果得到的频率分布直方图如图，则该班百米测试中成绩良好的人数有人47．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

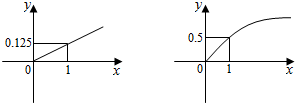    15．某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比，已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）．
    （1）分别写出两种产品的收益和投资的函数关系；
    （2）该家庭现有20万元资金，全部用于理财投资，问：怎样分配资金能使投资获得最大的收益，其最大收益为多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知函数$f（x）={log_9}（{9^x}+1）+kx（k∈R）$是偶函数．
    （1）求k的值；
    （2）若函数y=f（x）的图象与直线$y=\frac{1}{2}x+b$没有交点，求b的取值范围．
    （3）设$h（x）={log_9}（a•{3^x}-\frac{4}{3}a）$，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若对任意的x≥2，都有（x+a）|x+a|+（ax）|x|≤0，则a的最大值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．如果f（x）在[-5，5]上是奇函数，且f（3）＜f（1），则（　　）
    A．f（-1）＜f（-3）B．f（0）＞f（1）C．f（-1）＜f（1）D．f（-3）＜f（-5）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

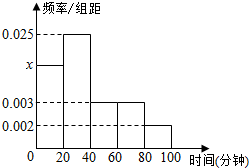    10．某中学随机抽取50名高一学生调查其每天运动的时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，运动
    的时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
    （1）求直方图中x的值；
    （2）定义运动的时间不少于1小时的学生称为“热爱运动”，若该校有高一学生1200人，请估计有多少学生“热爱运动”；
    （3）设m，n表示在抽取的50人中某两位同学每大运动的时间，且已知m，n∈[40，60）∪[80，100]，求事件“|m-n|＞20”的概率．

    查看答案和解析>>

    同步练习册答案